题目内容
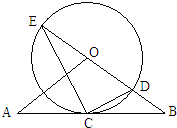
如图,直线D经过⊙O上的点C,并且OA=OB,CA=CB,直线OB交⊙O于点E、D,连接EC,CD.若tanE= ,⊙O上的半径为3,则OA的长为 .
,⊙O上的半径为3,则OA的长为 .
【答案】分析:先证证AB是⊙O的切线,只要连接OC,求证∠ACO=90°即可;再由三角形判定定理可知,△BCD∽△BEC,得BD与BC的比例关系,最后由切割线定理列出方程求出OA的长.
解答: 解:如图,连接OC,
解:如图,连接OC,
∵OA=OB,CA=CB,
∴OC⊥AB.
∴AB是⊙O的切线;
又∵BE是圆O割线,
∴BC2=BD•BE,
∵tan∠CED= ,
,
∴ =
= ,
,
∵△BCD∽△BEC,
∴ =
= =
= ,
,
设BD=x,BC=2x.又BC2=BD•BE,
∴(2x)2=x•(x+6),
解得x1=0,x2=2,
∵BD=x>0,
∴BD=2,
∴OA=OB=BD+OD=3+2=5
故答案为:5
点评:本题考查的是切线的判定、相似三角形的判定和性质,以及切割线定理的综合运用,属于基础题.
解答:
 解:如图,连接OC,
解:如图,连接OC,∵OA=OB,CA=CB,
∴OC⊥AB.
∴AB是⊙O的切线;
又∵BE是圆O割线,
∴BC2=BD•BE,
∵tan∠CED=
 ,
,∴
 =
= ,
,∵△BCD∽△BEC,
∴
 =
= =
= ,
,设BD=x,BC=2x.又BC2=BD•BE,
∴(2x)2=x•(x+6),
解得x1=0,x2=2,
∵BD=x>0,
∴BD=2,
∴OA=OB=BD+OD=3+2=5
故答案为:5
点评:本题考查的是切线的判定、相似三角形的判定和性质,以及切割线定理的综合运用,属于基础题.

练习册系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲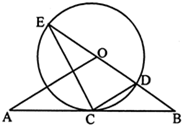 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连接EC、CD.
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连接EC、CD. 如图,直线D经过⊙O上的点C,并且OA=OB,CA=CB,直线OB交⊙O于点E、D,连接EC,CD.若tanE=
如图,直线D经过⊙O上的点C,并且OA=OB,CA=CB,直线OB交⊙O于点E、D,连接EC,CD.若tanE= 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CD,⊙O交直线OB于E,D,连接EC,CD.
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CD,⊙O交直线OB于E,D,连接EC,CD.