题目内容
在正三棱锥S-ABC中，异面直线AS与BC所成角的大小为________．
90°
分析：取AC中点E，连接SE，BE，由等腰三角形三线合一，可得SE⊥AC，BE⊥AC，进而由线面垂直的判定定理得到AE⊥面SBE，最后由线面垂直的性质得到AE⊥SB，进而可得角为90°
解答：
解：取AC中点E，连接SE，BE，∵SA=SC，∴SE⊥AC，同理得：BE⊥AC
∵SE∩BE=E，SE，BE?面SBE，∴AE⊥面SBE，
∵SB?面SBE，∴AE⊥SB
故直线SB与AC所成角为90°
故答案为：90°
点评：本题考查空间异面直线及其所成的角，解答的关键是熟练掌握空间线线垂直与线面垂直之间的相互转化．
分析：取AC中点E，连接SE，BE，由等腰三角形三线合一，可得SE⊥AC，BE⊥AC，进而由线面垂直的判定定理得到AE⊥面SBE，最后由线面垂直的性质得到AE⊥SB，进而可得角为90°
解答：
解：取AC中点E，连接SE，BE，∵SA=SC，∴SE⊥AC，同理得：BE⊥AC∵SE∩BE=E，SE，BE?面SBE，∴AE⊥面SBE，
∵SB?面SBE，∴AE⊥SB
故直线SB与AC所成角为90°
故答案为：90°
点评：本题考查空间异面直线及其所成的角，解答的关键是熟练掌握空间线线垂直与线面垂直之间的相互转化．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
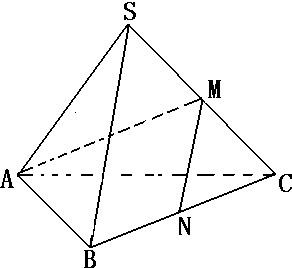如图，在正三棱锥S-ABC中，M、N分别为棱SC、BC的中点，并且AM⊥MN，若侧棱长SA=| 3 |
| A、9π | B、12π |
| C、16π | D、32π |
在正三棱锥S-ABC中，D是AB的中点，且SD与BC成45°角，则SD与底面ABC所成角的正弦为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|