题目内容
已知函数 ;
;
(1)若曲线y=f(x)在x=1和x=3处的切线平行,求a的值;
(2)求f(x)的单调区间;
(3)设g(x)=x2-2x,是否存在实数a,对?x1∈(0,2],?x2∈(0,2],使得f(x1)<g(x2)均成立;若存在,求a的取值范围;若不存在,请说明理由.
解:(1)
∵曲线y=f(x)在x=1和x=3处的切线平行
∴f′(1)=f′(3)
∴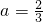
(2)函数的定义域为(0,+∞), =
=
当a=0时,单调减区间为(0,2),单调增区间为(2,+∞);
当 时,单调减区间为(2,
时,单调减区间为(2, ),单调增区间为(0,2),(
),单调增区间为(0,2),( ,+∞);
,+∞);
当 时,单调增区间为(0,+∞);
时,单调增区间为(0,+∞);
当a<0或 时,单调增区间为(0,
时,单调增区间为(0, ),(2,+∞);单调减区间为(
),(2,+∞);单调减区间为( ,2);
,2);
(3)由已知,转化为f(x)max<g(x)max.
由x∈(0,2],得到g(x)max=g(2)=0,
当a≤ 时,f(x)在(0,2]单调递增,此时f(x)max=f(2)=-2a-2+2ln2,
时,f(x)在(0,2]单调递增,此时f(x)max=f(2)=-2a-2+2ln2,
∴-2a-2+2ln2<0
∴ ,
,
当 时,f(x)在(0,
时,f(x)在(0, )上递增,在(
)上递增,在( ,2)上单调递减;
,2)上单调递减;
∴f(x)max=f( )=-2-
)=-2- -2lna,则-2-
-2lna,则-2- -2lna<0恒成立
-2lna<0恒成立
即只需 即可(∵
即可(∵ ,∴-2-2lna<0)
,∴-2-2lna<0)
综上可知,存在实数a满足条件,a的范围(ln2-1,+∞)
分析:(1)先求导函数,利用曲线y=f(x)在x=1和x=3处的切线平行,可求a的值;
(2)利用导数求函数的单调区间的步骤是①求导函数f′(x);②解f′(x)>0(或<0);③得到函数的增区间(或减区间),对于本题的在求单调区间时要注意函数的定义域以及对参数a的讨论情况;
(3)由题意可知f(x)的最大值小于g(x)的最大值,然后根据二次函数的增减性即可得到g(x)的最小值,再根据(2)求出的f(x)的单调区间,即可求出f(x)的最大值,进而列出关于a的不等式,求出不等式的解集即可得到a的范围.
点评:本题考查的重点是导数知识的运用,考查函数的单调性,考查函数的最值,考查恒成立问题,解题的难点是题意的理解与转化,体现了转化的思想.有一定的难度.

∵曲线y=f(x)在x=1和x=3处的切线平行
∴f′(1)=f′(3)
∴
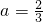
(2)函数的定义域为(0,+∞),
 =
=
当a=0时,单调减区间为(0,2),单调增区间为(2,+∞);
当
 时,单调减区间为(2,
时,单调减区间为(2, ),单调增区间为(0,2),(
),单调增区间为(0,2),( ,+∞);
,+∞);当
 时,单调增区间为(0,+∞);
时,单调增区间为(0,+∞);当a<0或
 时,单调增区间为(0,
时,单调增区间为(0, ),(2,+∞);单调减区间为(
),(2,+∞);单调减区间为( ,2);
,2);(3)由已知,转化为f(x)max<g(x)max.
由x∈(0,2],得到g(x)max=g(2)=0,
当a≤
 时,f(x)在(0,2]单调递增,此时f(x)max=f(2)=-2a-2+2ln2,
时,f(x)在(0,2]单调递增,此时f(x)max=f(2)=-2a-2+2ln2,∴-2a-2+2ln2<0
∴
 ,
,当
 时,f(x)在(0,
时,f(x)在(0, )上递增,在(
)上递增,在( ,2)上单调递减;
,2)上单调递减;∴f(x)max=f(
 )=-2-
)=-2- -2lna,则-2-
-2lna,则-2- -2lna<0恒成立
-2lna<0恒成立即只需
 即可(∵
即可(∵ ,∴-2-2lna<0)
,∴-2-2lna<0)综上可知,存在实数a满足条件,a的范围(ln2-1,+∞)
分析:(1)先求导函数,利用曲线y=f(x)在x=1和x=3处的切线平行,可求a的值;
(2)利用导数求函数的单调区间的步骤是①求导函数f′(x);②解f′(x)>0(或<0);③得到函数的增区间(或减区间),对于本题的在求单调区间时要注意函数的定义域以及对参数a的讨论情况;
(3)由题意可知f(x)的最大值小于g(x)的最大值,然后根据二次函数的增减性即可得到g(x)的最小值,再根据(2)求出的f(x)的单调区间,即可求出f(x)的最大值,进而列出关于a的不等式,求出不等式的解集即可得到a的范围.
点评:本题考查的重点是导数知识的运用,考查函数的单调性,考查函数的最值,考查恒成立问题,解题的难点是题意的理解与转化,体现了转化的思想.有一定的难度.

练习册系列答案
相关题目
 -2lnx、
-2lnx、 -2lnx、
-2lnx、 -2lnx、
-2lnx、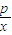 -2lnx、
-2lnx、