题目内容
函数 是R上的减函数,则a的取值范围是
是R上的减函数,则a的取值范围是
- A.(0,1)
- B.
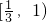
- C.
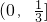
- D.
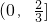
B
分析:先保证函数y=-x+3a在(0,+∞)是减函数,再保证函数y=ax在[0,+∞)上市减函数,最后只要使y=-x+3a的最大值大于或等于y=ax的最小值即可.
解答:有题意可得f(x)=ax是减函数
∴0<a<1
又∵ 是R上的减函数
是R上的减函数
∴当x=0时3a≥a0
即3a≥1
∴a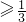
又∵0<a<1
∴
∴a的取值范围是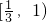
点评:分别判断出各段函数在其定义区间的单调性,再根据最值的大小保证函数在R上具有单调性.
分析:先保证函数y=-x+3a在(0,+∞)是减函数,再保证函数y=ax在[0,+∞)上市减函数,最后只要使y=-x+3a的最大值大于或等于y=ax的最小值即可.
解答:有题意可得f(x)=ax是减函数
∴0<a<1
又∵
 是R上的减函数
是R上的减函数∴当x=0时3a≥a0
即3a≥1
∴a
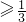
又∵0<a<1
∴

∴a的取值范围是
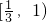
点评:分别判断出各段函数在其定义区间的单调性,再根据最值的大小保证函数在R上具有单调性.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 :函数
:函数 是R上的减函数,命题q:
是R上的减函数,命题q: 在
在 上的值域为
上的值域为 ,若“
,若“ ”为真命题,“
”为真命题,“ 是R上的减函数,则
是R上的减函数,则 的取值范围是
的取值范围是  是R上的减函数,命题q: 函数
是R上的减函数,命题q: 函数 在
在 的值域是 [-1,3].若“p且q”为假命题。“p或q” 为真命题,求
的值域是 [-1,3].若“p且q”为假命题。“p或q” 为真命题,求 的取值范围
的取值范围 是R上的减函数,命题q: 函数
是R上的减函数,命题q: 函数 在
在 的值域是 [-1,3].若“p且q”为假命题。“p或q” 为真命题,求
的值域是 [-1,3].若“p且q”为假命题。“p或q” 为真命题,求 的取值范围
的取值范围 是R上的减函数,
是R上的减函数, 上的值域为[-1,3],
上的值域为[-1,3], 的取值范围.
的取值范围.