题目内容
对于任意实数a(a≠0)和b,不等式|a+b|+|a-b|≥|a||x-1|恒成立,则实数x的取值范围是________.
[-1,3]
分析:由题意可得,|x-1|小于或等于 的最小值.利用不等式的性质求得
的最小值.利用不等式的性质求得 的最小值等于2,从而得到|x-1|≤2,由此求得实数x的取值范围.
的最小值等于2,从而得到|x-1|≤2,由此求得实数x的取值范围.
解答:由题意可得|x-1|≤ 恒成立,故|x-1|小于或等于
恒成立,故|x-1|小于或等于 的最小值.
的最小值.
∵ ≥
≥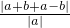 =2,故
=2,故 的最小值等于2.
的最小值等于2.
∴|x-1|≤2,
∴-2≤x-1≤2,解得-1≤x≤3,
故答案为[-1,3].
点评:本题主要考查绝对值不等式的解法,函数的恒成立问题,求出于 的最小值等于2,是解题的关键,体现了等价转化的数学思想,属于中档题.
的最小值等于2,是解题的关键,体现了等价转化的数学思想,属于中档题.
分析:由题意可得,|x-1|小于或等于
 的最小值.利用不等式的性质求得
的最小值.利用不等式的性质求得 的最小值等于2,从而得到|x-1|≤2,由此求得实数x的取值范围.
的最小值等于2,从而得到|x-1|≤2,由此求得实数x的取值范围.解答:由题意可得|x-1|≤
 恒成立,故|x-1|小于或等于
恒成立,故|x-1|小于或等于 的最小值.
的最小值.∵
 ≥
≥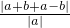 =2,故
=2,故 的最小值等于2.
的最小值等于2.∴|x-1|≤2,
∴-2≤x-1≤2,解得-1≤x≤3,
故答案为[-1,3].
点评:本题主要考查绝对值不等式的解法,函数的恒成立问题,求出于
 的最小值等于2,是解题的关键,体现了等价转化的数学思想,属于中档题.
的最小值等于2,是解题的关键,体现了等价转化的数学思想,属于中档题. 
练习册系列答案
相关题目