Question

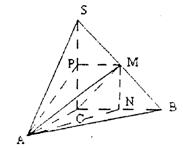
如图，在三棱锥S—ABC中，SC⊥平面ABC，点P、M分别是SC和SB的中点，设PM=AC=1，∠ACB=90°，直线AM与直线SC所成的角为60°。

（1）求证：平面MAP⊥平面SAC。

（2）求二面角M—AC—B的平面角的正切值；

  

Answer 1

（1）见解析（2）

解析:

（I）∵SC⊥平面ABC，SC⊥BC，又∵∠ACB=90°

∴AC⊥BC，AC∩SC=C，BC⊥平面SAC，

又∵P，M是SC、SB的中点

∴PM∥BC，PM⊥面SAC，∴面MAP⊥面SAC，　　　　

   （II）∵AC⊥平面SAC，∴面MAP⊥面SAC.

∴AC⊥CM，AC⊥CB，从而∠MCB为二面角M—AC－B的平面角，

∵直线AM与直线PC所成的角为60°

         ∴过点M作MN⊥CB于N点，连结AN，

则∠AMN=60°在△CAN中，由勾股定理得

         在Rt△AMN中，=

         在Rt△CNM中，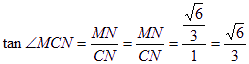

         故二面角M—AB—C的正切值为.