题目内容
已知函数f(x)=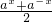 (a>0,a≠1,a为常数,x∈R).
(a>0,a≠1,a为常数,x∈R).
(1)若f(m)=6,求f(-m)的值;
(2)若f(1)=3,求f(2)的值.
解(1)∵f(-x)= =f(x)
=f(x)
∴f(x)为偶函数
∴f(-m)=f(m)=6.
(2)∵f(1)=3
∴a+ =6
=6
∴(a+ )2=36,即
)2=36,即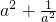 =34
=34
∴f(2)= =17
=17
分析:(1)由题设条件可证得,此函数是一个偶函数,又f(m)=6,直接根据偶函数的性质即可求得f(-m)的值;
(2)由于f(1)=3,可得到a+ =6,对此等式两边平方可得到
=6,对此等式两边平方可得到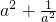 =34,又f(2)=
=34,又f(2)= ,由此可得出f(2)的值.
,由此可得出f(2)的值.
点评:本题考查函数奇偶性的性质及运用,有理数指数幂的运算,解题的关键是判断出函数的奇偶性及对指数式灵活变形求值,本题考查了变形求值的能力及推理判断的能力,属于基础题型.
 =f(x)
=f(x)∴f(x)为偶函数
∴f(-m)=f(m)=6.
(2)∵f(1)=3
∴a+
 =6
=6∴(a+
 )2=36,即
)2=36,即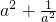 =34
=34∴f(2)=
 =17
=17分析:(1)由题设条件可证得,此函数是一个偶函数,又f(m)=6,直接根据偶函数的性质即可求得f(-m)的值;
(2)由于f(1)=3,可得到a+
 =6,对此等式两边平方可得到
=6,对此等式两边平方可得到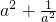 =34,又f(2)=
=34,又f(2)= ,由此可得出f(2)的值.
,由此可得出f(2)的值.点评:本题考查函数奇偶性的性质及运用,有理数指数幂的运算,解题的关键是判断出函数的奇偶性及对指数式灵活变形求值,本题考查了变形求值的能力及推理判断的能力,属于基础题型.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|