题目内容
已知函数f(x)=2|x|,若存在x∈R,使得不等式 成立,则实数k的最小值是
成立,则实数k的最小值是
- A.3
- B.2

- C.2
- D.

A
分析:由题意知这是一个存在性的问题,须求出不等式左边的最小值,令k大于等于左边的最小值,即可解出实数k的最小值.
解答:设F(x)= ,
,
由于F(-x)=F(x),
∴F(x)是偶函数,
当x≥0时,F(x)= ,
,
设x1>x2≥0,则F(x1)-F(x2)= -(
-( )
)
=(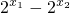 )×
)×
∵x1>x2≥0,∴ ,
, ,
,
∴F(x1)-F(x2)>0,
∴F(x)在[0,+∞)上是增函数,当x=0时,F(x)取得最小值3.
又F(x)是偶函数,其图象关于y轴对称,
∴当x∈R时,F(x)取得最小值3.
∵存在实数x使得不等式 成立,
成立,
∴k≥3,则实数k的最小值是3
故选A.
点评:本题考查不等关系与不等式,求解本题的关键是正确理解题意,区分存在问题与恒成立问题的区别,本题是一个存在问题,故取k≥3,即k大于等于左边的最小值即满足题意,本题是一个易错题,主要错误就是出在把存在问题当成恒成立问题求解导致错误.
分析:由题意知这是一个存在性的问题,须求出不等式左边的最小值,令k大于等于左边的最小值,即可解出实数k的最小值.
解答:设F(x)=
 ,
,由于F(-x)=F(x),
∴F(x)是偶函数,
当x≥0时,F(x)=
 ,
,设x1>x2≥0,则F(x1)-F(x2)=
 -(
-( )
)=(
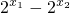 )×
)×
∵x1>x2≥0,∴
 ,
, ,
,∴F(x1)-F(x2)>0,
∴F(x)在[0,+∞)上是增函数,当x=0时,F(x)取得最小值3.
又F(x)是偶函数,其图象关于y轴对称,
∴当x∈R时,F(x)取得最小值3.
∵存在实数x使得不等式
 成立,
成立,∴k≥3,则实数k的最小值是3
故选A.
点评:本题考查不等关系与不等式,求解本题的关键是正确理解题意,区分存在问题与恒成立问题的区别,本题是一个存在问题,故取k≥3,即k大于等于左边的最小值即满足题意,本题是一个易错题,主要错误就是出在把存在问题当成恒成立问题求解导致错误.

练习册系列答案
相关题目