题目内容
已知函数![]() 的图象经过原点,且关于点
的图象经过原点,且关于点![]() 成中心对称.
成中心对称.
(1)求函数![]() 的解析式;
的解析式;
(2)若数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)在(2)的条件下,设数列![]() 的前
的前![]() 项和为
项和为![]() ,试判断
,试判断![]() 与
与![]() 的大小关系,并证
的大小关系,并证
明你的结论.
解:(1)因为函数![]() 的图象经过原点,
的图象经过原点,
所以![]() ,即
,即![]() .所以
.所以![]() .
.
因为函数![]() 的图象关于点
的图象关于点![]() 成中心对称,
成中心对称,
所以![]() .所以
.所以![]() .
.
(2)因为 ,且
,且![]() ,
,
所以 ,即
,即![]() ,即
,即![]() .
.
所以数列 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
所以![]() ,所以
,所以![]()
![]() .
.
(3)当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
所以![]()
![]() .
.
综上所述,![]()
![]() .
.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 的图象经过原点,且关于点(-1,1)成中心对称.
的图象经过原点,且关于点(-1,1)成中心对称. ,求数列{an}的通项公式;
,求数列{an}的通项公式;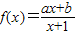 的图象经过原点,且关于点(-1,1)成中心对称.
的图象经过原点,且关于点(-1,1)成中心对称. ,求数列{an}的通项公式;
,求数列{an}的通项公式;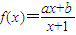 的图象经过原点,且关于点(-1,1)成中心对称.
的图象经过原点,且关于点(-1,1)成中心对称.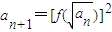 ,求数列{an}的通项公式;
,求数列{an}的通项公式;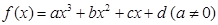 的图象经过原点,
的图象经过原点,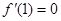 若
若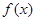 在
在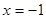 取得极大值2。
取得极大值2。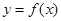 的解析式;
的解析式; ,求
,求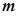 的最大值。
的最大值。 的图象经过原点,
的图象经过原点, 若
若 在
在 取得极大值2。
取得极大值2。 的解析式;
的解析式;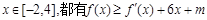 ,求
,求 的最大值。
的最大值。