题目内容
【选修4—4:坐标系与参数方程】
已知圆 的参数方程为
的参数方程为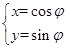 (
(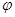 为参数),以坐标原点
为参数),以坐标原点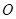 为极点,
为极点,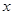 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为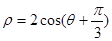 .
.
(I)将圆 的参数方程化为普通方程,将圆
的参数方程化为普通方程,将圆 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(II)圆 、
、 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
【答案】
(I)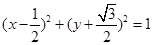 ;(II)|AB|=
;(II)|AB|=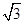
【解析】
试题分析:(I)由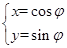 得x2+y2=1,
得x2+y2=1,
又∵ρ=2cos(θ+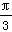 )=cosθ-
)=cosθ-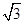 sinθ,
sinθ,
∴ρ2=ρcosθ-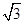 ρsinθ.
ρsinθ.
∴x2+y2-x+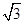 y=0,即
y=0,即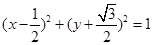
(II)圆心距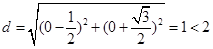 ,得两圆相交
,得两圆相交
由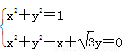 得,A(1,0),B
得,A(1,0),B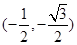 ,
,
∴|AB|=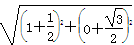 =
=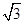
考点:本题主要考查极坐标方程与普通方程的互化,直线与圆的位置关系。
点评:中档题,学习参数方程、极坐标,其中一项基本的要求是几种不同形式方程的互化,其次是应用极坐标、参数方程,简化解题过程。参数方程的应用,往往可以把曲线问题转化成三角问题,也可在计算弦长时发挥较好作用。本题(II)利用“代数法”求弦长,也可考虑应用“特征直角三角形”,利用勾股定理求弦长。

练习册系列答案
相关题目
 为极点,
为极点, 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点 的直角坐标为
的直角坐标为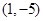 ,点
,点 的极坐标为
的极坐标为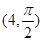 ,若直线
,若直线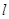 过点
过点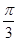 ,圆
,圆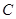 以
以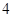 为半径。
为半径。