Question

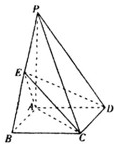（2012•泰安二模）如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，PA=AB=

2

，AD=1，点E是棱PB的中点．
（I）求证：平面ECD⊥平面PAD；
（II）求二面角A-EC-D的平面角的余弦值．

Answer 1

分析：（I）证明CD⊥平面PAD，利用面面垂直的判定，可证平面ECD⊥平面PAD；
（II）过点D作DF⊥CE，过点F作FG⊥CE，交AC于G，则∠DFG为所求的二面角的平面角，先利用AD⊥平面PAB，故AD⊥AE，从而求得DE，在Rt△CBE中，利用勾股定理求得CE，进而可知CE=CD推断出△CDE为等边三角形，求得DF，因为AE⊥平面PBC，故AE⊥CE，又FG⊥CE，知FG平行且等于AE的一半，从而求得FG，且G点为AC的中点，连接DG，则在Rt△ADC中，求得DG，最后利用余弦定理求得答案．

解答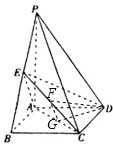：（I）证明：∵PA⊥平面ABCD，CD?平面ABCD，∴PA⊥CD，
∵底面ABCD为矩形，∴AD⊥CD
∵PA∩AD=A，∴CD⊥平面PAD
∵CD?平面ECD，
∴平面ECD⊥平面PAD；
（II）解：过点D作DF⊥CE，过点F作FG⊥CE，交AC于G，则∠DFG为所求的二面角的平面角．
∵AD⊥AB，AD⊥PA，AB∩PA=A，∴AD⊥平面PAB，∴AD⊥AE，从而DE=

AE2+AD2

=

2

在Rt△CBE中，CE=

BE2+BC2

=

2

，
∵CD=

2

，∴△CDE为等边三角形，故F为CE的中点，且DF=CD•sin60°=

6

2

因为AE⊥平面PBC，故AE⊥CE，又FG⊥CE，知FG∥AE．且FG=

1

2

AE，
从而FG=

1

2

，且G点为AC的中点，连接DG，则在Rt△ADC中，DG=

1

2

AD2+CD2

=

3

2

，
所以cos∠DFG=

DF2+FG2-DG2

2DF•FG

=

6

3

．

点评：本题考查面面垂直，考查面面角，解题的关键是掌握面面垂直的判定定理，正确作出面面角，求出三角形的三边，利用余弦定理求面面角．