题目内容
设椭圆 (a>b>0)的长半轴的长等于焦距,且x=4为它的右准线.
(a>b>0)的长半轴的长等于焦距,且x=4为它的右准线.
(I)求椭圆的方程;
(II)过定点M(m,0)(-2<m<2,m≠0为常数)作斜率为k(k≠0)的直线l与椭圆交于不同的两点A.B,问在x轴上是否存在一点N,使直线NA与NB的倾斜角互补?若存在,求出N点坐标,若不存在,请说明理由.
解:(Ⅰ)依题意得 解之得
解之得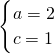 从而
从而 .
.
∴椭圆方程为 . …(4分)
. …(4分)
(Ⅱ)设直线l的方程为y=k(x-m),
联立方程得 消去y得(3+4k2)x2-8mk2x+4k2m2-12=0,…(6分)
消去y得(3+4k2)x2-8mk2x+4k2m2-12=0,…(6分)
∵△=64m2k4-16(k2m2-3)(3+4k2)=48k2(4-m2)+144>0.
设A(x1,y1),B(x2,y2),N(n,0),
则 ,
, ,(*)
,(*)
因为直线NA与NB的倾斜角互补等价于kNA+kNB=0,…(8分)
所以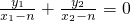 ,即
,即 ,…(9分)
,…(9分)
即2x1x2-(m+n)(x1+x2)+2mn=0,
将(*)式代入上式得 ,
,
整理得mn=4,∵m≠0,∴ ,所以,N点存在,且坐标为
,所以,N点存在,且坐标为 ,
,
因此,存在点N 使得直线NA与NB的倾斜角互补. …(12分)
使得直线NA与NB的倾斜角互补. …(12分)
分析:(I)直接利用长半轴的长等于焦距,且x=4为它的右准线列出关于a,b,c的方程,再求出a,b,c即可求出椭圆的方程;
(II)把 直线方程与椭圆方程联立求出点A.B的坐标和点N的坐标之间的关系,再结合直线NA与NB的倾斜角互补的对应结论kNA+kNB=0,即可求出N点坐标.
点评:本题主要考查直线与圆锥曲线的综合问题.解决这一类型题目的常用方法是:把直线方程与圆锥曲线方程联立,求出直线与圆锥曲线交点之间的关系;再结合其它条件来求对应结论.
 解之得
解之得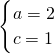 从而
从而 .
.∴椭圆方程为
 . …(4分)
. …(4分)(Ⅱ)设直线l的方程为y=k(x-m),
联立方程得
 消去y得(3+4k2)x2-8mk2x+4k2m2-12=0,…(6分)
消去y得(3+4k2)x2-8mk2x+4k2m2-12=0,…(6分)∵△=64m2k4-16(k2m2-3)(3+4k2)=48k2(4-m2)+144>0.
设A(x1,y1),B(x2,y2),N(n,0),
则
 ,
, ,(*)
,(*)因为直线NA与NB的倾斜角互补等价于kNA+kNB=0,…(8分)
所以
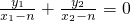 ,即
,即 ,…(9分)
,…(9分)即2x1x2-(m+n)(x1+x2)+2mn=0,
将(*)式代入上式得
 ,
,整理得mn=4,∵m≠0,∴
 ,所以,N点存在,且坐标为
,所以,N点存在,且坐标为 ,
,因此,存在点N
 使得直线NA与NB的倾斜角互补. …(12分)
使得直线NA与NB的倾斜角互补. …(12分)分析:(I)直接利用长半轴的长等于焦距,且x=4为它的右准线列出关于a,b,c的方程,再求出a,b,c即可求出椭圆的方程;
(II)把 直线方程与椭圆方程联立求出点A.B的坐标和点N的坐标之间的关系,再结合直线NA与NB的倾斜角互补的对应结论kNA+kNB=0,即可求出N点坐标.
点评:本题主要考查直线与圆锥曲线的综合问题.解决这一类型题目的常用方法是:把直线方程与圆锥曲线方程联立,求出直线与圆锥曲线交点之间的关系;再结合其它条件来求对应结论.

练习册系列答案
相关题目













 (“a>b〉0)的左焦点为
(“a>b〉0)的左焦点为 ,椭圆过点P(
,椭圆过点P( )
) 与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.
与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围. +
+ =1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.
=1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.