题目内容
下列四个命题中,真命题的序号有 (写出所有真命题的序号).①两个相互垂直的平面,一个平面内的任意一直线必垂直于另一平面内的无数条直线.
②圆x2+y2+4x+2y+1=0与直线y=
 x相交,所得弦长为2.
x相交,所得弦长为2.③若sin(α+β)=
 ,sin(α-β)=
,sin(α-β)= ,则tanαcotβ=5.
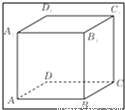
,则tanαcotβ=5.④如图,已知正方体ABCD-A1B1C1D1,P为底面ABCD内一动点,P到平面AA1D1D的距离与到直线CC1的距离相等,则P点的轨迹是抛物线的一部分.
【答案】分析:①利用面面垂直的性质判断.②利用直线和圆的位置关系判断.③利用两角和差的正弦公式求值.④利用抛物线的定义判断.
解答: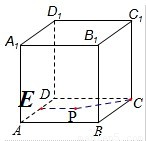 解:①根据面面垂直的性质可知,两个相互垂直的平面,一个平面内的任意一直线必垂直于另一平面内的无数条直线,所以①正确.
解:①根据面面垂直的性质可知,两个相互垂直的平面,一个平面内的任意一直线必垂直于另一平面内的无数条直线,所以①正确.
②圆的标准方程为(x+2)2+(y+1)2=4,圆心坐标为(-2,-1),半径为2.
因为圆心在直线y= x,所以直线与圆相交,相应的弦长为直径4,所以②错误.
x,所以直线与圆相交,相应的弦长为直径4,所以②错误.
③由sin(α+β)= ,sin(α-β)=
,sin(α-β)= ,得
,得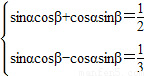 ,
,
解得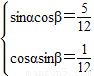 ,所以两式相除得tanαcotβ=5,所以③正确.
,所以两式相除得tanαcotβ=5,所以③正确.
④连结PC,则PC是点P到直线CC1的距离,过P作PE垂直于直线AD,则PE到平面AA1D1D的距离为PE,
因为P到平面AA1D1D的距离与到直线CC1的距离相等,所以PC=PE,满足抛物线的定义,
所以P点的轨迹是抛物线的一部分,所以④正确.
故正确的命题为①、③、④.
故答案为:①、③、④.
点评:本题主要考查命题的真假判断,牵扯的知识点较多,综合性较强.
解答:
 解:①根据面面垂直的性质可知,两个相互垂直的平面,一个平面内的任意一直线必垂直于另一平面内的无数条直线,所以①正确.
解:①根据面面垂直的性质可知,两个相互垂直的平面,一个平面内的任意一直线必垂直于另一平面内的无数条直线,所以①正确.②圆的标准方程为(x+2)2+(y+1)2=4,圆心坐标为(-2,-1),半径为2.
因为圆心在直线y=
 x,所以直线与圆相交,相应的弦长为直径4,所以②错误.
x,所以直线与圆相交,相应的弦长为直径4,所以②错误.③由sin(α+β)=
 ,sin(α-β)=
,sin(α-β)= ,得
,得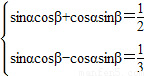 ,
,解得
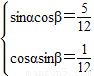 ,所以两式相除得tanαcotβ=5,所以③正确.
,所以两式相除得tanαcotβ=5,所以③正确.④连结PC,则PC是点P到直线CC1的距离,过P作PE垂直于直线AD,则PE到平面AA1D1D的距离为PE,
因为P到平面AA1D1D的距离与到直线CC1的距离相等,所以PC=PE,满足抛物线的定义,
所以P点的轨迹是抛物线的一部分,所以④正确.
故正确的命题为①、③、④.
故答案为:①、③、④.
点评:本题主要考查命题的真假判断,牵扯的知识点较多,综合性较强.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
(如图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是( )

| A、①② | B、②③ | C、②④ | D、③④ |
 (2012•厦门模拟)某赛季甲、乙两名篮球运动员各6场比赛得分情况用茎叶图记录,下列四个结论中,不正确的是( )
(2012•厦门模拟)某赛季甲、乙两名篮球运动员各6场比赛得分情况用茎叶图记录,下列四个结论中,不正确的是( )