题目内容
已知函数F(x)= ,(x
,(x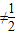 ),
),(I)求F(
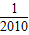 )+F(
)+F(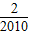 )+…+F(
)+…+F(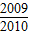 )的值;
)的值;(II)已知数列{an}满足a1=2,an+1=F(an),求证数列{
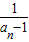 }是等差数列;
}是等差数列;(III)已知bn=
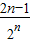 ,求数列{anbn}的前n项和Sn.
,求数列{anbn}的前n项和Sn.
【答案】分析:(I)由题意可得F(x)+F(1-x)=3,所以设S=F( )+f(
)+f( )+…+F(
)+…+F( )倒序后相加即可得到结果.
)倒序后相加即可得到结果.
(II)由a n+1=F(an)两边同减去1,得 =
= =2+
=2+ ,所以,{
,所以,{ }是以2为公差以1为首项的等差数列.
}是以2为公差以1为首项的等差数列.
(III)利用条件可得anbn= ,它是一个等差数列与等比数列积的形式,利用错位相减可求数列的和.
,它是一个等差数列与等比数列积的形式,利用错位相减可求数列的和.
解答:解:(I)因F(x)+F(1-x)= =3.------------------------------(2分)
=3.------------------------------(2分)
所以设S=F( )+f(
)+f( )+…+F(
)+…+F( )…(1)
)…(1)
S=F( )+f(
)+f( )+…+F(
)+…+F( )…(2)
)…(2)
(1)+(2)得:2S=2009×[F( )+F(
)+F( )]=3×2009=6027,
)]=3×2009=6027,
∴S= .
.
(II)由a n+1=F(an)两边同减去1,得a n+1-1= -1=
-1= .---------(7分)
.---------(7分)
所以 =
= =2+
=2+
所以,{ }是以2为公差以1为首项的等差数列.----(10分)
}是以2为公差以1为首项的等差数列.----(10分)
(III)因为 ,
,
∴an=1+ =
= .
.
因为bn= ,所以anbn=
,所以anbn= ------------------------------(12分)
------------------------------(12分)
Sn= +
+ +…+
+…+ (3)
(3)
 Sn=
Sn= +
+ +…+
+…+ (4)
(4)
由(3)-(4)得
 Sn=
Sn= +
+ +…+
+…+ -
-
=2- -
-
所以Sn=4- -----------------------------(14分)
-----------------------------(14分)
点评:本题主要考查了利用数列的递推公式构造等差数列,求解数列的通项公式,错位相减求解数列的和是数列求和方法中的重点与难点,要注意掌握
 )+f(
)+f( )+…+F(
)+…+F( )倒序后相加即可得到结果.
)倒序后相加即可得到结果.(II)由a n+1=F(an)两边同减去1,得
 =
= =2+
=2+ ,所以,{
,所以,{ }是以2为公差以1为首项的等差数列.
}是以2为公差以1为首项的等差数列.(III)利用条件可得anbn=
 ,它是一个等差数列与等比数列积的形式,利用错位相减可求数列的和.
,它是一个等差数列与等比数列积的形式,利用错位相减可求数列的和.解答:解:(I)因F(x)+F(1-x)=
 =3.------------------------------(2分)
=3.------------------------------(2分)所以设S=F(
 )+f(
)+f( )+…+F(
)+…+F( )…(1)
)…(1)S=F(
 )+f(
)+f( )+…+F(
)+…+F( )…(2)
)…(2)(1)+(2)得:2S=2009×[F(
 )+F(
)+F( )]=3×2009=6027,
)]=3×2009=6027,∴S=
 .
.(II)由a n+1=F(an)两边同减去1,得a n+1-1=
 -1=
-1= .---------(7分)
.---------(7分)所以
 =
= =2+
=2+
所以,{
 }是以2为公差以1为首项的等差数列.----(10分)
}是以2为公差以1为首项的等差数列.----(10分)(III)因为
 ,
,∴an=1+
 =
= .
.因为bn=
 ,所以anbn=
,所以anbn= ------------------------------(12分)
------------------------------(12分)Sn=
 +
+ +…+
+…+ (3)
(3) Sn=
Sn= +
+ +…+
+…+ (4)
(4)由(3)-(4)得
 Sn=
Sn= +
+ +…+
+…+ -
-
=2-
 -
-
所以Sn=4-
 -----------------------------(14分)
-----------------------------(14分)点评:本题主要考查了利用数列的递推公式构造等差数列,求解数列的通项公式,错位相减求解数列的和是数列求和方法中的重点与难点,要注意掌握

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|