Question

已知椭圆C的中心在原点，对称轴为坐标轴，且过（0，1），（1，）．

（Ⅰ）求椭圆C的方程；

（Ⅱ）直线l：3x﹣3y﹣1=0交椭圆C与A、B两点，若T（0，1）求证：．

Answer 1

考点：

直线与圆锥曲线的综合问题；椭圆的标准方程．

专题：

综合题．

分析：

（Ⅰ）设出椭圆C的方程，利用椭圆C过点过（0，1），（1，），建立方程组，即可求得椭圆C的方程；

（Ⅱ）由两边平方整理可得，故只需证明，将直线与椭圆方程联立，利用韦达定理，及向量的数量积即可得到结论．

解答：

（Ⅰ）解：设椭圆C的方程为mx²+ny²=1（m＞0．n＞0）

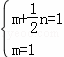由椭圆C过点过（0，1），（1，）得：，解得

∴椭圆C的方程为

（Ⅱ）证明：设A（x₁，y₁），B（x₂，y₂），由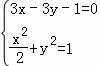消去y整理得27x²﹣12x﹣16=0，

由韦达定理得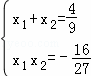

由两边平方整理可得，故只需证明

=x₁x₂+（y₁﹣1）（y₂﹣1）=x₁x₂+y₁y₂+（y₁+y₂）+1

而

∴=

故恒成立

点评：

本题考查待定系数法求椭圆的标准方程，考查直线与椭圆的位置关系，考查韦达定理的运用，解题的关键是联立方程，正确运用韦达定理．