题目内容
（本小题满分12分）
若函数
的定义域为
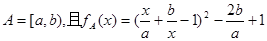，其中a、b为任
意正实数，且a<b。
（1）当A=
时，研究的单调性（不必证明）；
（2）写出的单调区间（不必证明），并求函数的最小值、最大值；
（3）若
其中k是正整数，对一切正整数k不等式
都有解，求m的取值范围。
【答案】
（1）当
是减函数，当
是增函数（2）减区间
增区间
，
最小值
，最大值
（3）
【解析】
试题分析：（1）当
∵
∴当是减函数，当是增函数
（2）
是减函数；在
上
是增函数。
∴当
有最小值为
当
有最大值为
（3）当A=Ik时
最小值为
当A= Ik+1时
最小值为
∴
设 
则 
∴
考点：函数求最值及不等式成立求函数范围
点评：第一二小题求最值应用到了均值不等式
，要注意验证等号成立条件；第三问不等式恒成立转化为求函数最值，这是函数综合题常用的转化思路
练习册系列答案
全优测试卷系列答案
冲刺100分1号卷系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
