题目内容
6.已知角α、β、γ构成公差为$\frac{π}{6}$的等差数列,若sinβ=$\frac{\sqrt{3}}{3}$,则sin2α+sin2γ=$\frac{5}{6}$.分析 首先根据已知条件,利用等差数列建立等量关系,$γ=β+\frac{π}{6}$,$α=β-\frac{π}{6}$代入关系式进行化简,最后求出结果.
解答 解:角α、β、γ构成公差为$\frac{π}{6}$的等差数列,
所以:α=β-$\frac{π}{6}$,$γ=β+\frac{π}{6}$,
则:sin2α+sin2γ=${sin}^{2}(β-\frac{π}{6})$+${sin}^{2}(β+\frac{π}{6})$
=$\frac{3}{4}{sin}^{2}β$+$\frac{3}{4}{sin}^{2}β$+$\frac{1}{4}{cos}^{2}β$+$\frac{1}{4}{cos}^{2}β$
=${sin}^{2}β+\frac{1}{2}$,
由于:$sinβ=\frac{\sqrt{3}}{3}$,
所以:${sin}^{2}β+\frac{1}{2}=\frac{5}{6}$
故答案为:$\frac{5}{6}$.
点评 本题考查的知识要点:等差数列性质的应用,三角函数关系式的恒等变换.和相关的运算问题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
16.已知复数z满足$\frac{1-2i}{z}$=i,则复数z的共轭复数在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.一个几何体的三视图如图所示,则这个几何体的外接球的表面积为 ( )
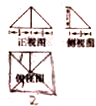

| A. | $\frac{4π}{3}$ | B. | $\frac{8π}{3}$ | C. | 4π | D. | 2π |
1.若l,m,n是不相同的空间直线,α,β是不重合的平面,则下列命题正确的是( )
| A. | α∥β,l?α,n?β⇒l∥n?????? | B. | l⊥n,m⊥n⇒l∥m | ||
| C. | l⊥α,l∥β⇒α⊥β | D. | α⊥β,l?α⇒l⊥β |
 如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA=SD,∠BAD=60°,AB=2,SE=$\sqrt{3}$,SC=$\sqrt{10}$,E是AD中点,SF=2FC.
如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA=SD,∠BAD=60°,AB=2,SE=$\sqrt{3}$,SC=$\sqrt{10}$,E是AD中点,SF=2FC.