题目内容
如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2,DE=1(1)求证:CE∥面ABF;
(2)若二面角A-BF-D的平面角的余弦值为
 ,求AB的长.
,求AB的长.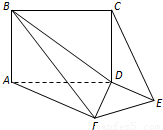
【答案】分析:(1)由矩形的对边平行,结合已知及面面平行的第二判定定理,可得面ABF∥面CDE,进而由面面平行的性质得到CE∥面ABF
(2)设AB=x,以F为原点,AF,EF所有直线分别为x,y轴建立空间坐标系,分别求出平面ABF和平面BFD的法向量,结合二面角A-BF-D的平面角的余弦值为 ,构造关于x的方程,解方程可得AB的长.
,构造关于x的方程,解方程可得AB的长.
解答:证明:(1)∵ABCD为矩形,
∴AB∥CD,
又∵AF∥DE,AB,AF?面ABF,AB∩AF=A,CD,DE?面CDE
∴面ABF∥面CDE
又∵CE?面CDE
∴CE∥面ABF;
(2)设AB=x,以F为原点,AF,EF所有直线分别为x,y轴建立空间坐标系,
∵AF=AD=2,DE=1
则F(0,0,0),A(-2,0,0),D(-1, ,0)
,0) ,B(-2,0,x)
,B(-2,0,x)
∴ =(1,-
=(1,- ,0),
,0), =(2,0,-x)
=(2,0,-x)
∵EF⊥平面ABF,
∴ =(0,1,0)为平面ABF的一个法向量
=(0,1,0)为平面ABF的一个法向量
设 =(a,b,c)为平面BFD的一个法向量,则
=(a,b,c)为平面BFD的一个法向量,则
 ,即
,即
令b=1,则 =(
=( ,1,
,1, )
)
∵cos< ,
, >=
>=
解得x=
∴AB=
点评:本题考查的知识点是直线与平面平行的判定,二面角的求法,熟练掌握空间线面关系判定的方法和步骤是解答(1)的关键.建立空间坐标系将二面角问题转化为向量夹角问题是解答(2)的关键.
(2)设AB=x,以F为原点,AF,EF所有直线分别为x,y轴建立空间坐标系,分别求出平面ABF和平面BFD的法向量,结合二面角A-BF-D的平面角的余弦值为
 ,构造关于x的方程,解方程可得AB的长.
,构造关于x的方程,解方程可得AB的长.解答:证明:(1)∵ABCD为矩形,
∴AB∥CD,
又∵AF∥DE,AB,AF?面ABF,AB∩AF=A,CD,DE?面CDE
∴面ABF∥面CDE
又∵CE?面CDE
∴CE∥面ABF;
(2)设AB=x,以F为原点,AF,EF所有直线分别为x,y轴建立空间坐标系,
∵AF=AD=2,DE=1
则F(0,0,0),A(-2,0,0),D(-1,
 ,0)
,0) ,B(-2,0,x)
,B(-2,0,x)∴
 =(1,-
=(1,- ,0),
,0), =(2,0,-x)
=(2,0,-x)∵EF⊥平面ABF,
∴
 =(0,1,0)为平面ABF的一个法向量
=(0,1,0)为平面ABF的一个法向量设
 =(a,b,c)为平面BFD的一个法向量,则
=(a,b,c)为平面BFD的一个法向量,则 ,即
,即
令b=1,则
 =(
=( ,1,
,1, )
)∵cos<
 ,
, >=
>=
解得x=

∴AB=

点评:本题考查的知识点是直线与平面平行的判定,二面角的求法,熟练掌握空间线面关系判定的方法和步骤是解答(1)的关键.建立空间坐标系将二面角问题转化为向量夹角问题是解答(2)的关键.

练习册系列答案
相关题目
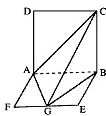 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF= 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且 (2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.
(2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.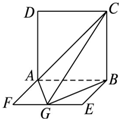 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=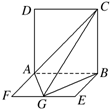 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=