题目内容
坐标平面中,向量
与向量
=(2,
)互相垂直且等长.请问下列哪些选项是正确的?
(1)向量
必为(
,-2)或(-
,2)
(2)向量
+
与
-
等长
(3)向量
+
与
的夹角可能为135°
(4)若向量
=a
+b
,其中,a,b为实数,则向量
的长度为
(5)若向量(1,0)=c
+d
,其中c,d为实数,则c>0.
| w |
| v |
| 5 |
(1)向量
| w |
| 5 |
| 5 |
(2)向量
| v |
| w |
| v |
| w |
(3)向量
| v |
| w |
| w |
(4)若向量
| u |
| v |
| w |
| u |
| a2+b2 |
(5)若向量(1,0)=c
| v |
| w |
(1)设
=(x,y),∵
⊥
?
•
=0?2x+
y=0①;
又∵|
|=|
|?
=
?x2+y2=9②;
由①②可得:(x,y)=(-
,2)或(
,-2),故结论正确;
(2)∵
+
=(2-
,
+2),
-
=(2+
,
-2),
∴|
+
|=|
-
|=
=
,故结论正确;
(3)设
+
与
的夹角为θ,则cosθ=
=
=
=
?θ=45°,
故(3)结论不正确;
(4)∵
=a
+b
=(2a-
b,
a+2b)或(2a+
b,
a-2b),
∴|
|=
=3
,故结论不正确;
(5)∵c
+d
=(1,0)?(2c-
d,
c+2d)=(1,0)或(2c+
d,
c-2d)=(1,0)?
或
?c=
,∴c>0结论正确;
| w |
| w |
| v |
| w |
| v |
| 5 |
又∵|
| w |
| v |
| x2+y2 |
22+(
|
由①②可得:(x,y)=(-
| 5 |
| 5 |
(2)∵
| v |
| w |
| 5 |
| 5 |
| v |
| w |
| 5 |
| 5 |
∴|
| v |
| w |
| v |
| w |
(2-
|
| 18 |
(3)设
| v |
| w |
| w |
(
| ||||||
|
|
| ||||||
|
|
|
| ||||||
|
|
| 1 | ||
|
故(3)结论不正确;
(4)∵
| u |
| v |
| w |
| 5 |
| 5 |
| 5 |
| 5 |
∴|
| u |
(2a-
|
| a2+b2 |
(5)∵c
| v |
| w |
| 5 |
| 5 |
| 5 |
| 5 |
|
|
| 2 |
| 9 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
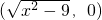 ,O为坐标原点,若实数λ使向量
,O为坐标原点,若实数λ使向量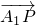 ,
,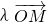 和
和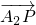 满足:
满足: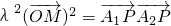 ,设点P的轨迹为W.
,设点P的轨迹为W.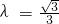 时,过点A1且斜率为1的直线与W相交的另一个交点为B,能否在直线x=-9上找到一点C,恰使△A1BC为正三角形?请说明理由.
时,过点A1且斜率为1的直线与W相交的另一个交点为B,能否在直线x=-9上找到一点C,恰使△A1BC为正三角形?请说明理由.