题目内容
(本小题满分14分) 求
至少有一个负实根的充要条件。
至少有一个负实根的充要条件。
。试题分析：（1）
时为一元一次方程，其根为
，符合题目要求；…..3分（2）当
时，为一元二次方程，它有实根的充要条件是判断式
，即
，从而。………….6分①又设方程
的两根为
，则由韦达定理得
。因而方程有一个负实根的充要条件是
，得
。……..9分①②方程
有两个负根的充要条件是
，即
。….12分综上，
至少有一个负实根的充要条件是：………..14分点评：⑴本题主要考查一个一元二次方程根的分布问题．在二次项系数不确定的情况下，一定要分二次项系数分为0和不为0两种情况讨论．
⑵设一元二次方程
（
）的两个实根为
，
，且
。①
，
(两个正根)
；②
，
(两个负根)
；③
(一个正根一个负根)
。
练习册系列答案
发散思维新课堂系列答案
相关题目
的根一个在
内，一个在
内，一个在
内.（12分）
的实数解的个数为_______.
在
上有四个不同的根
，则
．
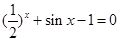，下列命题中：(1) 该方程没有小于0的实数解；(2) 该方程有无数个实数解；(3) 该方程在(–∞，0)内有且只有一个实数解；
在区间
上单调，且
，则方程
唯一的零点在区间（1，3）、（1，4）、（1，5）内，那么下列命题中错误的是（ ）
内有零点 
满足：①
，
②
③
则
的值是 . 
有实数解
，则
