题目内容
甲船在岛A的正南B处,以4km/h的速度向正北方向航行,AB=10km,同时乙船自岛A出发以6km/h的速度向北偏东60°的方向去,当甲、乙两船相距最近时,它们所航行的时间为
- A.
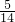 h
h - B.
 h
h - C.2 h
- D.2.15 h
A
分析:两船轨迹及距离最近时两船连线构成一个以B岛为顶点,角度是120度的三角形,设距离最近时航行时间为t(h),此时距离s(km),此时甲船到B岛距离为(10-4t)km,乙船距离B岛6t(km).cos120°= =-0.5,化简得:s2=28t2-20t+100,由此能求出甲、乙两船相距最近时,它们的航行时间.
=-0.5,化简得:s2=28t2-20t+100,由此能求出甲、乙两船相距最近时,它们的航行时间.
解答:解:两船轨迹及距离最近时两船连线构成一个以B岛为顶点,角度是120度的三角形,
设距离最近时航行时间为t(h),此时距离s(km),此时甲船到B岛距离为(10-4t)km,乙船距离B岛6t(km).
由余弦定理可得 cos120°= =-0.5,化简得:s2=28t2-20t+100.
=-0.5,化简得:s2=28t2-20t+100.
此函数的图象是抛物线,开口朝上,故在对称轴处s2有最小值,故s2取最小值时,t=- =
=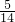 小时.
小时.
故选A.
点评:本题考查解三角形问题在生产实际中的具体运用,解题时要认真审题,仔细解答,注意余弦定理的灵活运用,属于中档题.
分析:两船轨迹及距离最近时两船连线构成一个以B岛为顶点,角度是120度的三角形,设距离最近时航行时间为t(h),此时距离s(km),此时甲船到B岛距离为(10-4t)km,乙船距离B岛6t(km).cos120°=
 =-0.5,化简得:s2=28t2-20t+100,由此能求出甲、乙两船相距最近时,它们的航行时间.
=-0.5,化简得:s2=28t2-20t+100,由此能求出甲、乙两船相距最近时,它们的航行时间.解答:解:两船轨迹及距离最近时两船连线构成一个以B岛为顶点,角度是120度的三角形,
设距离最近时航行时间为t(h),此时距离s(km),此时甲船到B岛距离为(10-4t)km,乙船距离B岛6t(km).
由余弦定理可得 cos120°=
 =-0.5,化简得:s2=28t2-20t+100.
=-0.5,化简得:s2=28t2-20t+100.此函数的图象是抛物线,开口朝上,故在对称轴处s2有最小值,故s2取最小值时,t=-
 =
=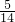 小时.
小时.故选A.
点评:本题考查解三角形问题在生产实际中的具体运用,解题时要认真审题,仔细解答,注意余弦定理的灵活运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 h
h h
h