Question

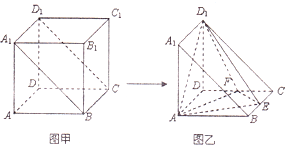将棱长为a的正方体截去一半（如图甲所示）得到如图乙所示的几何体，点E，F分别是BC，DC的中点．
（1）证明：AF⊥ED₁；
（2）求三棱锥E-AFD₁的体积．

Answer 1

分析：（1）连接DE，交AF于点O，先证明D₁D⊥AF，再证明AF⊥DE，可得AF⊥平面D₁DE，从而可得AF⊥ED₁；
（2）利用VE-AFD1=VD1-AEF=

1

3

S△AEF•D1D，即可求三棱锥E-AFD₁的体积．

解答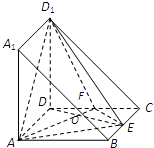：（1）证明：连接DE，交AF于点O
∵D₁D⊥平面ABCD，AF?平面ABCD，∴D₁D⊥AF…（2分）
∵点E，F分别是BC，D₁C的中点，∴DF=CE
又∵AD=DC，∠ADF=∠DCE=90°
∴△ADF≌△DCE，∴∠AFD=∠DEC
又∵∠CDE+∠DEC=90°，∴∠CDE+∠AFD=90°
∴∠DOF=180°-（∠CDE+∠AFD）=90°，即AF⊥DE…（5分）
又∵D₁D∩DE=D，∴AF⊥平面D₁DE，
又∵ED₁?平面D₁DE，∴AF⊥ED₁；  …（6分）
（2）解：∵D₁D⊥平面ABCD，∴D₁D是三棱锥D₁-AEF的高，且D₁D=a
∵点E，F分别是BC，D₁C的中点，∴DF=CF=CE=BE=

a

2

…（7分）
∴S△AEF=a2-

1

2

AD•DF-

1

2

CF•CE-

1

2

AB•BE=

3a2

8

…（10分）
∴VE-AFD1=VD1-AEF=

1

3

S△AEF•D1D=

1

3

•

3a2

8

•a=

a3

8

…（12分）

点评：本题考查线面垂直的判定，考查三棱锥体积的计算，转换底面是求三棱锥体积的关键，属于中档题．