题目内容
设m,n是两条不同直线,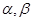 是两个不同的平面,给出下列四个命题
是两个不同的平面,给出下列四个命题
①若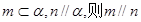 ②
②
③若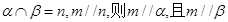 ④若
④若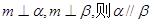
其中正确的命题是 ( )
| A.① | B.② | C.③④ | D.②④ |
D
解析试题分析:①考查线面平行的性质,当线面平行时,直线与平面内任意直线平行或异面,因此错误;②由线面垂直的性质即两面垂直的判定可知正确;③错误,直线 还可能在平面
还可能在平面 内;④依据面面平行的判定可知是正确的
内;④依据面面平行的判定可知是正确的
考点:空间线面平行垂直的判定
点评:正确求解本题需要对空间线面平行垂直的判定方法熟练掌握,包括各种判定性质定理及二级结论

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
直线在平面外是指
| A.直线与平面没有公共点 | B.直线与平面相交 |
| C.直线与平面平行 | D.直线与平面最多只有一个公共点 |
已知直线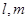 和平面
和平面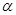 , 则下列命题正确的是
, 则下列命题正确的是
A.若 ∥ ∥ , ,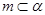 ,则 ,则 ∥ ∥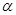 | B.若 ∥ ∥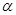 , ,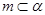 ,则 ,则 ∥ ∥ |
C.若 ⊥ ⊥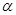 , ,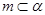 ,则 ,则 ⊥ ⊥ | D.若 ⊥ ⊥ , , ⊥ ⊥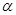 ,则 ,则 ∥ ∥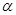 |
设 为两条直线,
为两条直线, 为两个平面,下列说法正确的是( )
为两个平面,下列说法正确的是( )
A.若 ,则 ,则 |
B.若  |
C. |
D.若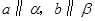 , , ,则 ,则 |
已知正方体 中,
中, 、
、 分别为
分别为 、
、 的中点,则异面直线
的中点,则异面直线 与
与 所成角的余弦值为( )
所成角的余弦值为( )
A. | B. | C. | D.0 |
已知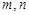 是两条不同直线,
是两条不同直线,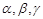 是三个不同平面,下列命题中正确的是( )
是三个不同平面,下列命题中正确的是( )
A.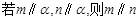 | B.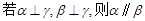 |
C.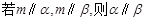 | D.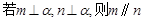 |
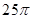
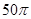
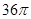
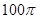
 是两个不同的平面,则下列四个命题中是真命题的是( )
是两个不同的平面,则下列四个命题中是真命题的是( )



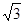 ,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).
,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).