题目内容
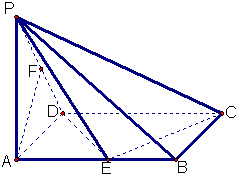
在四棱锥P－ABCD中，底面ABCD为正方形，且边长为2a，棱PD⊥底面ABCD，PD=2b，取各侧棱的中点E，F，G，H，写出点E，F，G，H的坐标．解析: 由图形知，DA⊥DC，DC⊥DP，DP⊥DA，故以D为原点，建立如图空间坐标系D－xyz．
因为E，F，G，H分别为侧棱中点，由立体几何知识可知，平面EFGH与底面ABCD平行，
从而这4个点的竖坐标都为P的竖坐标的一半，也就是b，
由H为DP中点，得H（0，0，b）
E在底面面上的投影为AD中点，所以E的横坐标和纵坐标分别为a和0，所以E（a，0，b），
同理G（0，a，b）；
F在坐标平面xOz和yOz上的投影分别为点E和G，故F与E横坐标相同都是a，
与G的纵坐标也同为a，又F竖坐标为b，故F（a，a，b）．
练习册系列答案
黄冈创优卷系列答案
相关题目
已知在四棱锥P一ABCD中，底面ABCD是矩形，PA⊥平面ABCD，
如图．在四棱锥P一ABCD中，底面ABCD是正方形，侧棱PD⊥底 面ABCD，PD=DC=2，E是PC的中点．
已知在四棱锥P一ABCD中，二面角P一AD一B为60°，∠PDA=45°，∠DAB=90°，∠PAD=90°，∠ADC=135°，
如图，在四棱锥P一ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点．PA=PD=AD=2，点M在线段PC上 PM=
（本小题满分14分）在四棱锥P－ABCD中，底面ABCD是正方形，侧棱PD与底面ABCD垂直，PD=DC，E是PC的中点，作EF
于点F（Ⅰ）证明PA
平面EBD．
平面EFD．
的余弦值；