题目内容
（2012•茂名一模）已知向量
=(cosx+sinx，sinx)，
=(cosx+sinx，-2sinx)，且f(x)=
•
．
（1）求f（x）的解析式和它的最小正周期；
（2）求函数f(x)在x∈[0，
]的值域．
| a |
| b |
| a |
| b |
（1）求f（x）的解析式和它的最小正周期；
（2）求函数f(x)在x∈[0，
| π |
| 2 |
分析：（1）由向量的坐标运算可求得f（x）=
sin（2x+
），从而可求得它的最小正周期；
（2）由0≤x≤
，可求得
≤2x+
≤
，利用正弦函数的单调性即可求得函数f(x)在x∈[0，
]的值域．
| 2 |
| π |
| 4 |
（2）由0≤x≤
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
| π |
| 2 |
解答：解：（1）∵f（x）=（cosx+sinx）2-2sin2x
=1+sin2x-（1-cos2x）
=sin2x+cos2x
=
sin（2x+
），
∴函数的最小正周期T=
=π；
（2）∵0≤x≤
，
∴
≤2x+
≤
，
∴-
≤sin（2x+
）≤1，
∴-1≤
sin（2x+
）≤
．
∴函数f(x)在x∈[0，
]的值域为[-1，
]．
=1+sin2x-（1-cos2x）
=sin2x+cos2x
=
| 2 |
| π |
| 4 |
∴函数的最小正周期T=
| 2π |
| 2 |
（2）∵0≤x≤
| π |
| 2 |
∴
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
∴-
| ||
| 2 |
| π |
| 4 |
∴-1≤
| 2 |
| π |
| 4 |
| 2 |
∴函数f(x)在x∈[0，
| π |
| 2 |
| 2 |
点评：本题考查平面向量数量积的坐标表示，考查三角函数中的恒等变换应用，考查正弦函数的周期及复合三角函数的单调性，属于三角中的综合，属于中档题．
练习册系列答案
相关题目
（2012•茂名一模）如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题：
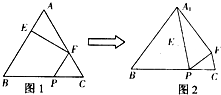（2012•茂名一模）如图1，在正三角形ABC中，AB=3，E、F、P分别是AB、AC、BC边上的点，AE=CF=CP=1．将△AFE沿折起到△A1EF的位置，使平面A1EF与平面BCFE垂直，连接A1B、A1P（如图2）．
（2012•茂名一模）如图，设P是圆x2+y2=2上的动点，点D是P在x轴上的投影．M为线段PD上一点，且