题目内容
已知函数f(x)的定义域为R,f(0)=1,对任意x∈R都有 =
=
- A.

- B.
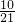
- C.

- D.
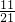
B
分析:由f(0)=1,且f(x+1)=f(x)+2,得f(n+1)-f(n)=2,f(10)=21.所以 .由此能求出结果.
.由此能求出结果.
解答:由f(0)=1且,f(x+1)=f(x)+2,
得f(n+1)-f(n)=2,f(10)=21.
所以 .
.
所以 .
.
故选B.
点评:本题考查数列与函数问题的综合应用,考查数列、不等式知识,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.
分析:由f(0)=1,且f(x+1)=f(x)+2,得f(n+1)-f(n)=2,f(10)=21.所以
 .由此能求出结果.
.由此能求出结果.解答:由f(0)=1且,f(x+1)=f(x)+2,
得f(n+1)-f(n)=2,f(10)=21.
所以
 .
.所以
 .
.故选B.
点评:本题考查数列与函数问题的综合应用,考查数列、不等式知识,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
