题目内容
函数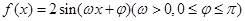 的部分图象如图所示,其 中A,B两点之间的距离为5,则f(x)的递增区间是
的部分图象如图所示,其 中A,B两点之间的距离为5,则f(x)的递增区间是
A.[6k-1,6k+2](k Z) Z) | B.[6k-4,6k-1](k Z) Z) |
C.[3k-1,4k+2](k Z) Z) | D.[3k-4,3k-1](k Z) Z) |
B
解析试题分析: ,所以
,所以 ,即
,即 ,所以
,所以 ,
, 由
由 过点
过点 ,即
,即 ,
, ,
,
解得 ,函数为
,函数为 ,由
,由 ,
,
解得 ,故函数单调递增区间为
,故函数单调递增区间为 .
.
考点:函数 的解析式;函数
的解析式;函数 单调性。
单调性。
点评:做此题的关键是根据图像求出函数的解析式。已知函数 的图像求解析式,是常见题型。一般的时候,(1)先求A;根据最值;(2)在求
的图像求解析式,是常见题型。一般的时候,(1)先求A;根据最值;(2)在求 :根据周期;(3)最后求
:根据周期;(3)最后求 :找到代入。
:找到代入。

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
若 ,则
,则 的值为
的值为
| A.0 | B. | C.1 | D. |
要得到函数 的图象,只要将函数
的图象,只要将函数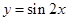 的图象( )
的图象( )
A.向左平移 单位 单位 | B.向右平移 单位 单位 |
C.向右平移 单位 单位 | D.向左平移 单位 单位 |
已知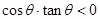 ,则角
,则角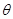 是( )
是( )
| A.第一象限角或第二象限角 | B.第二象限角或地三象限角 |
| C.第三象限角或第四象限角 | D.第四象限角或第一象限角 |
将函数 的图象向左平移
的图象向左平移 个单位,所得图象的解析式是( )
个单位,所得图象的解析式是( )
A. | B. |
C. | D. |
为了得到函数 的图像,只要把函数
的图像,只要把函数 图象上所有的点( )
图象上所有的点( )
A.向左平行移动 个单位长度 个单位长度 | B.向右平行移动 个单位 个单位 |
C.向左平行移动 个单位长度 个单位长度 | D.向右平行移动 个单位 个单位 |
函数 导函数的图象如图所示,则下列说法正确的是( )
导函数的图象如图所示,则下列说法正确的是( )
A.函数 的递增区间为 的递增区间为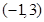 |
B.函数 的递减区间为 的递减区间为 |
C.函数 在 在 处取得极大值 处取得极大值 |
D.函数 在 在 处取得极小值 处取得极小值 |
函数f(x)=  sin2x-2sin2x,(0≤x≤π/2)则函数f(x)的最小值为
sin2x-2sin2x,(0≤x≤π/2)则函数f(x)的最小值为
| A.1 | B.-2 | C. | D.-  |
角 的终边经过点
的终边经过点 (
( ,
, )(
)( ),则
),则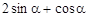 的值是( )
的值是( )
A.1或 | B. 或 或 | C.1或 | D. 或 或 |