题目内容
设函数f(x)=x2-2x-1在区间(t,t+1)上有最小值g(t),求g(t)的解析式.
思路解析:考虑f(x)=x2-2x-1的对称轴x=1与区间(t,t+1)的位置关系,结合二次函数在区间上的最大值、最小值求解.
解:f(x)=(x-1)2-2,对称轴为x=1.
(1)当x=1∈(t,t+1),即0≤t≤1时,g(t)=f(1)=-2;
(2)当t>1时,f(x)在区间(t,t+1)上是增函数,g(t)=f(t)=t2-2t-1;
(3)当t+1<1,即t<0时,f(x)在区间(t,t+1)上是减函数,g(t)=f(t+1)=t2-2.
综上所述,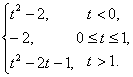

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 设函数
设函数 设函数
设函数