题目内容
设函数f(x)=ax2+bx+1,a>0,b∈R 的最小值为-a,f(x)=0两个实根为x1、x2.(1)求x1-x2的值;
(2)若关于x的不等式f(x)<0解集为A,函数f(x)+2x在A上不存在最小值,求a的取值范围;
(3)若-2<x1<0,求b的取值范围.
【答案】分析:(1)由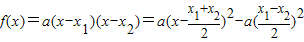 ,知
,知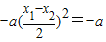 ,由此能求出x1-x2的值.
,由此能求出x1-x2的值.
(2)设x1<x2,f(x)+2x=ax2-(a(x1+x2)-2)x+ax1x2,在(x1,x2)不存在最小值,由此能求出a的取值范围.
(3)由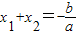 ,
,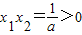 ,知
,知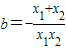 .由此能求出b的取值范围.
.由此能求出b的取值范围.
解答:解:(1)∵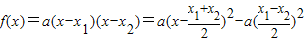
∴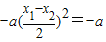
∴x1-x2=±2.(4分)
(2)不妨设x1<x2;f(x)+2x=ax2-(a(x1+x2)-2)x+ax1x2,在(x1,x2)不存在最小值,
∴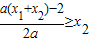 或
或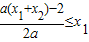 (8分)
(8分)
又x2-x1=2,a>0∴0<a≤1(10分)
(3)∵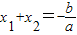 ,
,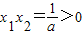
∴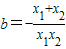 (12分)
(12分)
又-2<x1<0
∴x2=x1-2
∴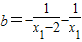 在x1∈(-2,0)上为增函数.
在x1∈(-2,0)上为增函数.
∴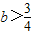 (16分)
(16分)
点评:本昰考查二次函数的性质,解题时要认真审题,仔细解答,注意合理地进行等价转化.
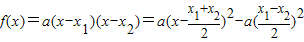 ,知
,知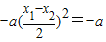 ,由此能求出x1-x2的值.
,由此能求出x1-x2的值.(2)设x1<x2,f(x)+2x=ax2-(a(x1+x2)-2)x+ax1x2,在(x1,x2)不存在最小值,由此能求出a的取值范围.
(3)由
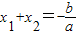 ,
,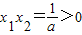 ,知
,知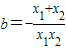 .由此能求出b的取值范围.
.由此能求出b的取值范围.解答:解:(1)∵
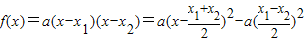
∴
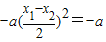
∴x1-x2=±2.(4分)
(2)不妨设x1<x2;f(x)+2x=ax2-(a(x1+x2)-2)x+ax1x2,在(x1,x2)不存在最小值,
∴
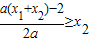 或
或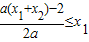 (8分)
(8分)又x2-x1=2,a>0∴0<a≤1(10分)
(3)∵
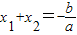 ,
,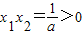
∴
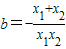 (12分)
(12分)又-2<x1<0
∴x2=x1-2
∴
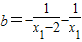 在x1∈(-2,0)上为增函数.
在x1∈(-2,0)上为增函数.∴
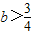 (16分)
(16分)点评:本昰考查二次函数的性质,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
 设函数f(x)=(a
设函数f(x)=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |