题目内容
已知函数f(x)=(Ⅰ)当a>2时,求函数f(x)的单调递减区间;
(Ⅱ)当a≤1时,求函数y=f(x)的图像与直线y=2的交点个数.
证明:(Ⅰ)f′(x)= ax2-(a+2)x+2.
∵f′(x)<0![]() ax2-(a+2)x+2<0.
ax2-(a+2)x+2<0.
由a>2,有![]() >1.∴f′(x)<0
>1.∴f′(x)<0![]()
![]() <x<1.
<x<1.
∴f(x)的递减区间为(![]() ,1).
,1).
[注:若写成闭区间也正确.]
(Ⅱ)由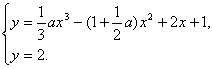 消去y,有
消去y,有
![]() ax3-(1+
ax3-(1+![]() a)x2+2x-1=0.(*)
a)x2+2x-1=0.(*)
y=f(x)的图像与直线y=2的交点个数问题化归为方程(*)解的个数问题.
令g(x)=![]() ax3-(1+
ax3-(1+![]() a)x2+2x-1,
a)x2+2x-1,
则g′(x)= ax2-(a+2)x+2=(ax-2)(x-1).
1°当a=0时,g(x)=-(x-1)2,此时g(x)与x轴只有一个交点;
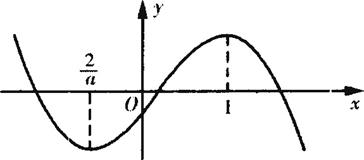
2°当a<0时,g′(x)>0![]()
![]() <x<1.
<x<1.
g′(x)<0![]() x>1或x<
x>1或x<![]() .
.
g(x)的极大值g(1)=![]() >0.
>0.
g(x)的极小值g(![]() )=
)=![]() -1<0.
-1<0.
[注:当x→-∞时,g(x)>0;当x→+∞时,g(x)<0.不要求学生能写出.]
∴a<0时,g(x)的图像与x轴有三个交点.
3°当0<a≤1时,g′(x)>0![]() x>
x>![]() 或x<1;
或x<1;
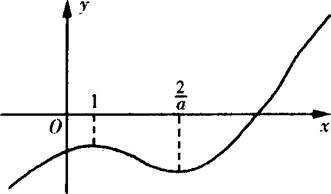
g′(x)<0![]() 1<x<
1<x<![]() .
.
g(x)的极大值g(1)=![]() <0;
<0;
g(x)的极小值g(![]() )=
)=![]() -1=
-1=![]() <0.
<0.
[注:x→+∞时,g(x)>0.]
∴g(x)的图像与x轴只有一个交点.
综上所述,当0≤a≤1时,函数y=f(x)的图像与直线y=2只有一个交点;当a<0时,有三个交点.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |