Question

一个棱锥的三视图如图（尺寸的长度单位为m），则该棱锥的全面积是（单位：m²）．（　　）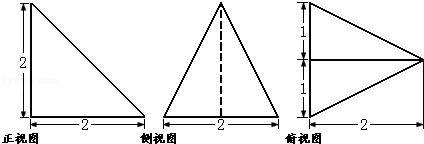

A．

B．

C．

D．

Answer 1

考点：

由三视图求面积、体积．

专题：

计算题；图表型．

分析：

由三视图可以看出，此几何体是一个侧面与底面垂直的三棱锥，垂直于底面的侧面是一个高为2，底连长也为2的等腰直角三角形，底面与垂直于底面的侧面全等，此两面的面积易求，另两个与底面不垂直的侧面是全等的，可由顶点在底面上的射影作出此两侧面底边的高，将垂足与顶点连接，此线即为侧面三角形的高线，求出侧高与底面的连长，用三角形面积公式求出此两侧面的面积，将四个面的面积加起来即可

解答：

解：由三视图可以看出，此几何体是一个侧面与底面垂直且底面与垂直于底面的侧面全等的三棱锥

由图中数据知此两面皆为等腰直角三角形，高为2，底面连长为2，故它们的面积皆为=2，

由顶点在底面的投影向另两侧面的底边作高，由等面积法可以算出，此二高线的长度长度相等，为，

将垂足与顶点连接起来即得此两侧面的斜高，由勾股定理可以算出，此斜高为2，同理可求出侧面底边长为，

可求得此两侧面的面积皆为=，

故此三棱锥的全面积为2+2++=，

故选A．

点评：

本题考点是由三视图求几何体的面积、体积，考查对三视图的理解与应用，主要考查对三视图与实物图之间的关系，用三视图中的数据还原出实物图的数据，再根据相关的公式求表面积与体积，本题求的是三棱锥的全面积，做本题时要注意本题中的规律应用，即四个侧面两两相等，注意到这一点，可以大大降低运算量．三视图的投影规则是主视、俯视 长对正；主视、左视高平齐，左视、俯视 宽相等．