题目内容
已知椭圆 +
+ =1(a>b>0),点P(
=1(a>b>0),点P( a,
a, a)在椭圆上.
a)在椭圆上.
(1)求椭圆的离心率;
(2)设A为椭圆的左顶点,O为坐标原点,若点Q在椭圆上且满足|AQ|=|AO|,求直线OQ的斜率的值.
(1)  (2) k=±
(2) k=±
解析解:(1)∵点P( a,
a, a)在椭圆上,
a)在椭圆上,
∴ +
+ =1整理得
=1整理得 =
= .
.
∴e= =
=
=
= =
=
= .
.
(2)由题意可知,点A坐标为(-a,0),|AO|=a.
设直线OQ的斜率为k,
则其方程为y=kx,
设点Q坐标为(x0,y0).
则
消去y0,整理得 =
= ①
①
由|AQ|=|AO|得(x0+a)2+k2 =a2.
=a2.
整理得(1+k2 2ax0=0.
2ax0=0.
由于x0≠0,
得x0=- .②
.②
把②代入①得 =
= ,
,
整理得(1+k2)2=4k2· +4.
+4.
由(1)知 =
= ,
,
故(1+k2)2= k2+4,
k2+4,
即5k4-22k2-15=0,
解得k2=5.
∴直线OQ的斜率k=± .
.

练习册系列答案
相关题目
 =1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
=1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
 的离心率为
的离心率为 ,短轴长是2.
,短轴长是2.
 时,求k的取值范围.
时,求k的取值范围. -
- =1(b∈N*)的左、右两个焦点为F1、F2,P是双曲线上的一点,且满足|PF1||PF2|=|F1F2|2,|PF2|<4.
=1(b∈N*)的左、右两个焦点为F1、F2,P是双曲线上的一点,且满足|PF1||PF2|=|F1F2|2,|PF2|<4. 的一个顶点
的一个顶点 为直角顶点作此椭圆的内接等腰直角三角形
为直角顶点作此椭圆的内接等腰直角三角形 ,试问:(1)这样的等腰直角三角形是否存在?若存在,写出一个等腰直角三角形两腰所在的直线方程。若不存在,说明理由。(2)这样的等腰直角三角形若存在,最多有几个?
,试问:(1)这样的等腰直角三角形是否存在?若存在,写出一个等腰直角三角形两腰所在的直线方程。若不存在,说明理由。(2)这样的等腰直角三角形若存在,最多有几个? 的焦点为
的焦点为 ,点
,点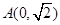 ,线段
,线段 的中点在抛物线上.设动直线
的中点在抛物线上.设动直线 与抛物线相切于点
与抛物线相切于点 ,且与抛物线的准线相交于点
,且与抛物线的准线相交于点 ,以
,以 为直径的圆记为圆
为直径的圆记为圆 .
. 的值;
的值; 轴的位置关系;
轴的位置关系; ,使得圆
,使得圆
 .
. 的任意两点,E为线段AB的中点,射线OE交椭圆C于点P.设
的任意两点,E为线段AB的中点,射线OE交椭圆C于点P.设 =t
=t ,求实数t的值.
,求实数t的值.