题目内容
已知f(x)是偶函数,且在(-∞,0]上单调递减,对任意x∈R,x≠0,都有f(x)+f( )=-1+2log2(x2+
)=-1+2log2(x2+ ),
),
(1)指出f(x)在[0,+∞)上的单调性(不要求证明),并求f(1)的值;
(2)k为常数,-1<k<1,解关于x的不等式 。
。
 )=-1+2log2(x2+
)=-1+2log2(x2+ ),
),(1)指出f(x)在[0,+∞)上的单调性(不要求证明),并求f(1)的值;
(2)k为常数,-1<k<1,解关于x的不等式
 。
。 解:(1)f(x)在[0,+∞)上是增函数.
∵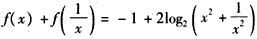 ,
,
∴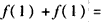
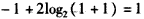 ,
,
∴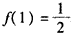 。
。
(2)因为f(x)是偶数,所以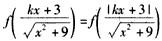 ,
,
故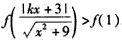 ,
,
∵f(x)在[0,+∞)上是增函数,
∴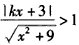 ,∴
,∴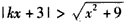 ,
,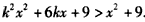 ,
,
∴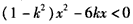 ,
,
①若k=0,则x2<0,∴不等式解集为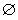 ;
;
②若-1<k<0,则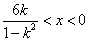 ,∴不等式解集为
,∴不等式解集为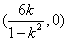 ;
;
③若0<k<1,则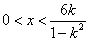 ,∴不等式解集为
,∴不等式解集为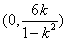 。
。
∵
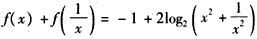 ,
,∴
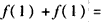
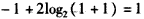 ,
,∴
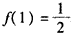 。
。(2)因为f(x)是偶数,所以
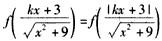 ,
,故
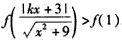 ,
,∵f(x)在[0,+∞)上是增函数,
∴
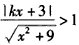 ,∴
,∴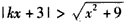 ,
,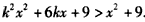 ,
,∴
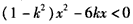 ,
,①若k=0,则x2<0,∴不等式解集为
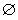 ;
;②若-1<k<0,则
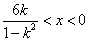 ,∴不等式解集为
,∴不等式解集为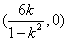 ;
;③若0<k<1,则
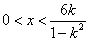 ,∴不等式解集为
,∴不等式解集为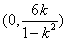 。
。 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,1]恒成立,则实数a的取值范围是
,1]恒成立,则实数a的取值范围是