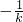题目内容
设对于任意的x,都有f(-x)=-f(x),f′(-x0)=-k≠0,则f′(x0)=( )
| A、k | ||
| B、-k | ||
C、
| ||
D、-
|
分析:利用奇偶函数导数之间的关系可以很快给出答案:奇函数的导函数是偶函数,偶函数的导函数是奇函数.
解答:解:由已知条件可知该函数为奇函数,其导函数为偶函数,这是因为:对f(-x)=-f(x)两边求导数得到:
f′(-x)=-f′(x),
而根据复合函数求导法则又可得到f′(-x)=-f′(-x),
因此f′(-x)=f′(x).故f′(x0)=f′(-x0)=-k;
故选B.
f′(-x)=-f′(x),
而根据复合函数求导法则又可得到f′(-x)=-f′(-x),
因此f′(-x)=f′(x).故f′(x0)=f′(-x0)=-k;
故选B.
点评:本题考查导函数的奇偶性.可以利用图象得出导函数的奇偶性,也可利用复合函数求导法则证明出导函数的奇偶性.

练习册系列答案
相关题目
 )=________.
)=________.