题目内容
定义在R上的函数f（x）满足下列三个条件：（1）f（x+3）=-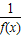
；（2）对任意3≤x1＜x2≤6，都有f（x1）＜f（x2）；（3）y=f（x+3）的图象关于y轴对称．则下列结论中正确的是（ ）A．f（3）＜f（7）＜f（4.5）
B．f（3）＜f（4.5）＜f（7）
C．f（7）＜f（4.5）＜f（3）
D．f（7）＜f（3）＜f（4.5）
【答案】分析：先由f（x+3）=-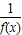
，得函数周期为6，得到f（7）=f（1）；再利用y=f（x+3）的图象关于y轴对称得到y=f（x）的图象关于x=3轴对称，进而得到f（1）=f（5）；最后利用条件（2）得出结论．
解答：解：因为f（x+3）=-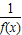
，
所以f（x+6）=-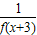
=-
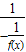=f（x）；
即函数周期为6，故f（7）=f（1）．
又因为y=f（x+3）的图象关于y轴对称，
所以y=f（x）的图象关于x=3轴对称．
所以f（1）=f（5）．
又对任意3≤x1＜x2≤6，都有f（x1）＜f（x2）；
所以f（3）＜f（4.5）＜f（5）=f（1）=f（7）．
故选B．
点评：本题主要考查函数奇偶性，周期性与单调性的综合问题．解决本题的关键有两处：①由f（x+3）=-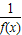
，得函数周期为6；②由y=f（x+3）的图象关于y轴对称得到y=f（x）的图象关于x=3轴对称．
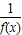，得函数周期为6，得到f（7）=f（1）；再利用y=f（x+3）的图象关于y轴对称得到y=f（x）的图象关于x=3轴对称，进而得到f（1）=f（5）；最后利用条件（2）得出结论．解答：解：因为f（x+3）=-
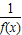，所以f（x+6）=-
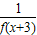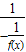=-=f（x）；即函数周期为6，故f（7）=f（1）．
又因为y=f（x+3）的图象关于y轴对称，
所以y=f（x）的图象关于x=3轴对称．
所以f（1）=f（5）．
又对任意3≤x1＜x2≤6，都有f（x1）＜f（x2）；
所以f（3）＜f（4.5）＜f（5）=f（1）=f（7）．
故选B．
点评：本题主要考查函数奇偶性，周期性与单调性的综合问题．解决本题的关键有两处：①由f（x+3）=-
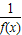，得函数周期为6；②由y=f（x+3）的图象关于y轴对称得到y=f（x）的图象关于x=3轴对称． 
练习册系列答案
相关题目