题目内容
已知 ,函数
,函数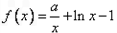 (其中
(其中 为自然对数的底数).
为自然对数的底数).
(1)求函数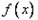 在区间
在区间 上的最小值;
上的最小值;
(2)设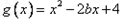 ,当
,当 时,若对任意
时,若对任意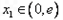 ,存在
,存在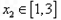 ,使得
,使得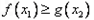 ,求实数
,求实数 的取值范围.
的取值范围.
 ,函数
,函数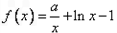 (其中
(其中 为自然对数的底数).
为自然对数的底数). (1)求函数
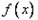 在区间
在区间 上的最小值;
上的最小值; (2)设
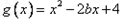 ,当
,当 时,若对任意
时,若对任意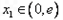 ,存在
,存在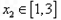 ,使得
,使得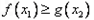 ,求实数
,求实数 的取值范围.
的取值范围.解:(1) ∵
∴
若 时, 函数
时, 函数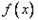 在区间
在区间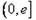 是减函数
是减函数  ;
;
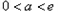 时 函数
时 函数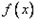 在区间
在区间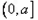 是减函数,
是减函数, 是增函数
是增函数  ;
;
(2)由(1)可知, 时,函数
时,函数 在
在 的最小值为0,
的最小值为0,
∴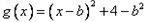
当 时,
时, 不成立
不成立
当 时,
时, 恒成立
恒成立
当 时,
时,
此时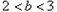
综上知,满足条件的实数 的取值范围
的取值范围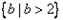

∴

若
 时, 函数
时, 函数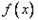 在区间
在区间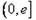 是减函数
是减函数  ;
; 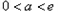 时 函数
时 函数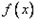 在区间
在区间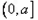 是减函数,
是减函数, 是增函数
是增函数  ;
;(2)由(1)可知,
 时,函数
时,函数 在
在 的最小值为0,
的最小值为0, ∴
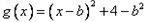
当
 时,
时, 不成立
不成立 当
 时,
时, 恒成立
恒成立当
 时,
时,
此时
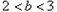
综上知,满足条件的实数
 的取值范围
的取值范围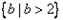

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
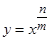 ,其中
,其中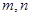 是取自集合
是取自集合 的两个不同值,则该函数为偶函数的概率为_____.
的两个不同值,则该函数为偶函数的概率为_____.