题目内容

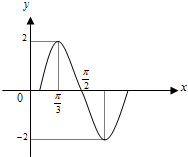
精英家教网已知函数y=Asin（ωx+φ）+b（A＞0，|φ|＜π，b为常数）的一段图象（如图）所示．
（1）求函数的解析式；
（2）求这个函数的单调区间．
分析：（1）图象中给出了半个周期的完整图象，故可得
T
2
=
π
2
-(-
π
3
)=
5π
6
．解出周期T，由公式求ω，又最高点与最低点的纵坐标的差为3，可得|A|=
3
2
进而求出A，b，到此函数解析式可以表示为y=
3
2
sin(
6
5
x+φ)+
3
2
，将点(
π
2
，0)代入y=
3
2
sin(
6
5
x+φ)+
3
2
求φ
（2）根据正弦函数的单调性，令相位属于[2kπ-
π
2
， 2kπ+
π
2
]，k∈z求函数的增区间，令相位属于[2kπ+
π
2
， 2kπ+
3π
2
]，k∈z求函数的减区间．
解答：解：（1）由已知，如图
A=
1
2
(ymax-ymin)=
3
2
，
T
2
=
π
ω
=
π
2
-(-
π
3
)=
5π
6
，ω=
6
5
．易知b=
3
2

∴y=
3
2
sin(
6
5
x+φ)+
3
2
，
将点(
π
2
，0)代入y=
3
2
sin(
6
5
x+φ)+
3
2
得sin(
3π
5
+φ)=-1
即
3π
5
+φ=2kπ-
π
2
，k∈z解得φ=2kπ-
11π
10
(k∈Z)
又|φ|＜π，当k=1时，φ=
9π
10
＜π
∴y=
3
2
sin(
6
5
x+
9π
10
)+
3
2
．
（2）令2kπ-
π
2
≤
6
5
x+
9π
10
≤2kπ+
π
2
得
5kπ
3
-
7π
6
≤x≤
5kπ
3
-
π
3

令2kπ+
π
2
≤
6
5
x+
9π
10
≤2kπ+
3π
2
得
5kπ
3
-
π
3
≤x≤
5kπ
3
+
π
2
．(k∈Z)
∴[
5kπ
3
-
7π
6
，
5kπ
3
-
π
3
](k∈Z)是单调递增区间，
  [
5kπ
3
-
π
3
，
5kπ
3
+
π
2
](k∈Z)．是单调递减区间．
点评：本题考点是三角函数的图象与性质，考查知道了三角函数图象上的特征求三角函数的解析式，以及根据三角函数的解析式求三角函数的单调区间，是三角函数的图象与性质中常规题型．
练习册系列答案
相关题目
已知函数y=Asin（ωx+φ），在同一周期内，当x=
π
12
时，取最大值y=2，当x=
7π
12
时，取得最小值y=-2，那么函数的解析式为（　　）
A、y=
1
2
sin（x+
π
3
）
B、y=2sin（2x+
π
3
）
C、y=2sin（
x
2
-
π
6
）
D、y=2sin（2x+
π
6
）
精英家教网已知函数y=Asin（ωx+∅）（A＞0，ω＞0，-π≤∅≤π）一个周期的图象（如图），则这个函数的一个解析式为（　　）
A、y=2sin(
3
2
x+
π
2
)
B、y=2sin(3x+
π
6
)
C、y=2sin(3x-
π
6
)
D、y=2sin(3x-
π
2
)
已知函数y=Asin(ωx+?)+B(A＞0，ω＞0，|?|＜
π
2
)的周期为T，在一个周期内的图象如图所示，则φ=
-
π
6
-
π
6
．
已知函数y=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜
π
2
)的一部分图象如图所示，则（　　）
已知函数y=Asin（ωx+∅）+k的最大值为4，最小值为0，最小正周期是
π
2
，在x∈[
π
24
，
π
12
]上单调递增，则下列符合条件的解析式是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网