题目内容
已知函数y=loga(x-1)+3(a>0,a≠1)所过定点的横、纵坐标分别是等差数列{an}的第二项与第三项,若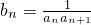 ,数列{bn}的前n项和为Tn,则T10=
,数列{bn}的前n项和为Tn,则T10=
- A.

- B.

- C.1
- D.
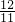
B
分析:由函数的解析式求得定点的坐标为(2,3),可得等差数列{an}的公差d=1,通项公式为an=n,求得数列{bn}的通项公式为bn= -
- ,由此求得数列{bn}的前n项和.
,由此求得数列{bn}的前n项和.
解答:函数y=loga(x-1)+3(a>0,a≠1)所过定点的坐标为(2,3),
由题意可得 a3=3,a2=2,故等差数列{an}的公差d=1,通项公式为an=n.
故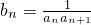 =
= =
= -
- =
= -
- .
.
故 T10= +
+ +
+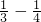 +…+
+…+ =1-
=1- =
= ,
,
故选B.
点评:本题主要考查对数函数的图象过定点问题,等差数列的通项公式,用裂项法求数列的前n项和,属于中档题.
分析:由函数的解析式求得定点的坐标为(2,3),可得等差数列{an}的公差d=1,通项公式为an=n,求得数列{bn}的通项公式为bn=
 -
- ,由此求得数列{bn}的前n项和.
,由此求得数列{bn}的前n项和.解答:函数y=loga(x-1)+3(a>0,a≠1)所过定点的坐标为(2,3),
由题意可得 a3=3,a2=2,故等差数列{an}的公差d=1,通项公式为an=n.
故
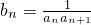 =
= =
= -
- =
= -
- .
.故 T10=
 +
+ +
+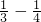 +…+
+…+ =1-
=1- =
= ,
,故选B.
点评:本题主要考查对数函数的图象过定点问题,等差数列的通项公式,用裂项法求数列的前n项和,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 7、已知函数y=loga(x+b)的图象如图所示,则a、b的取值范围分别是( )
7、已知函数y=loga(x+b)的图象如图所示,则a、b的取值范围分别是( )