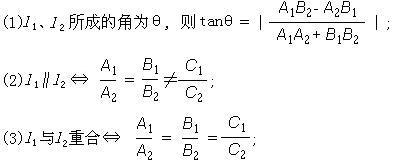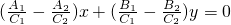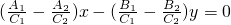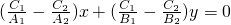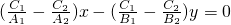题目内容
已知直线：A1x+B1y+C1=0（C1≠0）与直线l2：A2x+B2y+C2=0（C2≠0）交于点M，O为坐标原点，则直线OM的方程为（ ）A．
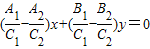
B．
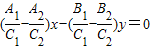
C．
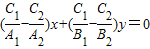
D．
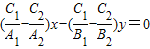
【答案】分析：将两直线的一般式中的常数项均变为1，验证O、M的坐标是否均满足该直线的方程即可判断．
解答：解：
x+
y+1=0，
l2：
x+
y+1=0，
两式相减得（
-
）x+（
-
）y=0．
∵点O、M的坐标都满足该直线的方程，
∴点O、M都在该直线上，
∴直线OM的方程为（
-
）x+（
-
）y=0．
故选A．
点评：本题考查两条直线的交点坐标，考查转化思想与分析验证能力，属于难题．
解答：解：
x+y+1=0，l2：
x+y+1=0，两式相减得（
-）x+（-）y=0．∵点O、M的坐标都满足该直线的方程，
∴点O、M都在该直线上，
∴直线OM的方程为（
-）x+（-）y=0．故选A．
点评：本题考查两条直线的交点坐标，考查转化思想与分析验证能力，属于难题．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
已知直线l1：A1x+B1y+C1=0，l2：A2x+B2y+C2=0，则
=
是l1∥l2的（ ）
| A1 |
| B1 |
| A2 |
| B2 |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
A
