题目内容
5.(1)设A={-4,2a-1,a2},B={a-5,1-a,9},已知A∩B={9},求a的值,并求出A∪B.(2)已知集合A={x|-3≤x≤5},B={x|m-2≤x≤m+1},满足B⊆A,求实数m的取值范围.
分析 (1)A,B,以及两集合的交集,得到9属于A,根据A中的元素列出关于a的方程,求出方程的解得到a的值,进而求出A与B的并集即可;
(2)由A,B,以及B为A的子集,确定出m的范围即可.
解答 解 (1)∵A={-4,2a-1,a2},B={a-5,1-a,9},A∩B={9},
∴9∈A,
∴a2=9或2a-1=9,
解得:a=±3或a=5,
当a=3时,A={9,5,-4},B={-2,-2,9},B中元素违背了互异性,舍去;
当a=-3时,A={9,-7,-4},B={-8,4,9},A∩B={9}满足题意,
此时A∪B={-7,-4,-8,4,9};
当a=5时,A={25,9,-4},B={0,-4,9},此时A∩B={-4,9},
与A∩B={9}矛盾,故舍去,
综上所述,a=-3,A∪B={-7,-4,-8,4,9};
(2)∵A={x|-3≤x≤5},B={x|m-2≤x≤m+1},且B⊆A
∴B≠∅,要满足B⊆A,须有$\left\{\begin{array}{l}-3≤m-2\\ m+1≤5\end{array}\right.$,
解得:-1≤m≤4.
点评 此题考查了并集及其运算,集合的包含关系判断及其应用,熟练掌握并集的定义是解本题的关键.

练习册系列答案
相关题目
16.已知全集U={1,2,3,4,5,6,7},A={2,4,6},B={1,3,5,6,7},则A∩(∁UB)等于( )
| A. | {2,4,6} | B. | {1,3,5} | C. | {2,4} | D. | {2,5} |
13.直线l:y=x-1的倾斜角是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{4}$ |
14. 如图,四边形ABCD为矩形,AB=$\sqrt{3}$,BC=1,以A为圆心,1为半径作四分之一个圆弧DE,在∠DAB内任作射线AP,则射线AP与线段BC有公共点的概率为( )
如图,四边形ABCD为矩形,AB=$\sqrt{3}$,BC=1,以A为圆心,1为半径作四分之一个圆弧DE,在∠DAB内任作射线AP,则射线AP与线段BC有公共点的概率为( )
 如图,四边形ABCD为矩形,AB=$\sqrt{3}$,BC=1,以A为圆心,1为半径作四分之一个圆弧DE,在∠DAB内任作射线AP,则射线AP与线段BC有公共点的概率为( )
如图,四边形ABCD为矩形,AB=$\sqrt{3}$,BC=1,以A为圆心,1为半径作四分之一个圆弧DE,在∠DAB内任作射线AP,则射线AP与线段BC有公共点的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
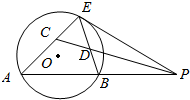 如图,过圆外一点P的直线交圆O于A、B两点,PE是圆O的切线,CP平分∠APE,分别与AE、BE交于点C,D.
如图,过圆外一点P的直线交圆O于A、B两点,PE是圆O的切线,CP平分∠APE,分别与AE、BE交于点C,D.