题目内容
已知函数f(x)=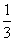 ax3+bx2+2x-1,g(x)=-x2+x+1,若函数f(x)的图象与函数g(x)的图象的一个公共点P的横坐标为1,且两曲线在点P处的切线互相垂直。
ax3+bx2+2x-1,g(x)=-x2+x+1,若函数f(x)的图象与函数g(x)的图象的一个公共点P的横坐标为1,且两曲线在点P处的切线互相垂直。
(1)求实数a,b的值;
(2)对任意x1,x2∈[-1,1],不等式f(x1)+k<g(x2)恒成立,求实数k的取值范围。
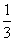 ax3+bx2+2x-1,g(x)=-x2+x+1,若函数f(x)的图象与函数g(x)的图象的一个公共点P的横坐标为1,且两曲线在点P处的切线互相垂直。
ax3+bx2+2x-1,g(x)=-x2+x+1,若函数f(x)的图象与函数g(x)的图象的一个公共点P的横坐标为1,且两曲线在点P处的切线互相垂直。(1)求实数a,b的值;
(2)对任意x1,x2∈[-1,1],不等式f(x1)+k<g(x2)恒成立,求实数k的取值范围。
解:(1)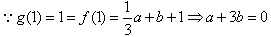 ,
,
又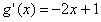 ,
,
∴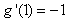 ,
,
∵两曲线在点P处的切线互相垂直,
∴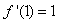 ,
,
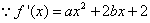 ,
,
∴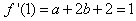 ,
,
∴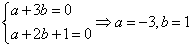 。
。
(2)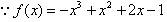 ,
,
对任意的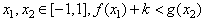 恒成立
恒成立
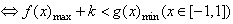 ,
,
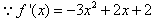 ,
,
则f′(x)>0得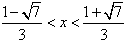 ,
,
∴函数f(x)在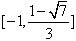 上递减,在
上递减,在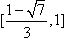 上递增,
上递增,
而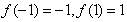 ,
,
∴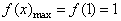 ,
,
而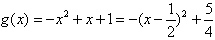 ,
,
当x∈[-1,1]时,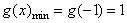 ,
,
故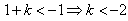 ;
;
∴实数k的取值范围是(-∞,-2)。
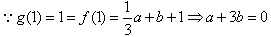 ,
,又
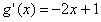 ,
,∴
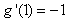 ,
,∵两曲线在点P处的切线互相垂直,
∴
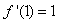 ,
, 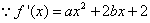 ,
,∴
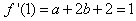 ,
,∴
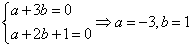 。
。(2)
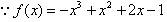 ,
,对任意的
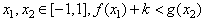 恒成立
恒成立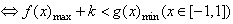 ,
,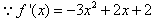 ,
,则f′(x)>0得
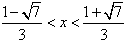 ,
,∴函数f(x)在
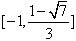 上递减,在
上递减,在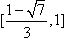 上递增,
上递增,而
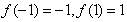 ,
,∴
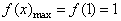 ,
,而
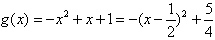 ,
, 当x∈[-1,1]时,
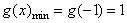 ,
,故
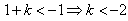 ;
;∴实数k的取值范围是(-∞,-2)。

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目