Question

在球内有相距9cm的两个平行截面，面积分别为49π cm²和400π cm²，求此球的半径．

Answer 1

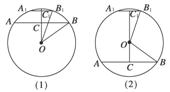
[解析]　①若两截面位于球心的同侧，如图(1)所示的是经过球心O的大圆截面，C、C₁分别是两平行截面的圆心，设球的半径为R，截面圆的半径分别为r、r₁.

由πr＝49π，得r₁＝7，由πr²＝400π，得r＝20.

在Rt△OB₁C₁中，OC₁＝＝，

在Rt△OBC中，OC＝＝.

由题意可知，OC₁－OC＝9，

即－＝9，

解得R＝25.

②若球心在两截面之间，如图(2)所示，

OC₁＝，OC＝.

由题意可知，OC₁＋OC＝9，

即＋＝9，

＝9－，

整理，得＝－15，此方程无解，

综上所述，此球的半径为25cm.