题目内容
已知三棱柱A1B1C1—ABC的底面边长及侧棱长均相等,AB⊥CB1,且侧面ABB1A1垂直于底面ABC.(1)求证:平面ABC1⊥平面CBB1C1;
(2)求侧棱B1B与底面ABC所成角的大小.
剖析:(1)利用面面垂直的判定定理,关键是在一个平面内找另一个平面的垂线(这条直线是CB1);(2)利用面面垂直的性质定理,作出侧棱B1B与底面ABC所成的角.
(1)证明:∵BB1C1C是菱形,∴CB1⊥C1B.
又∵AB⊥CB1,AB∩C1B=B,
∴CB1⊥平面ABC1.
而CB1![]() 平面CBB1C1,
平面CBB1C1,
∴平面ABC1⊥平面CBB1C1.
(2)解:作B1D⊥AB于D,连结CD.
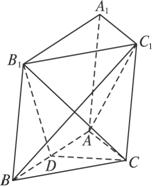
∵侧面ABB1A1⊥底面ABC,而平面ABB1A1∩平面ABC=AB,
∴B1D⊥面ABC.
∴∠B1BD就是侧棱B1B与底面ABC所成的角.
又∵CB1⊥AB,∴其射影CD⊥AB.
而△ABC是正三角形,∴BD=![]() AB=
AB=![]() B1B.
B1B.
∴∠B1BD=60°,即侧棱B1B与底面ABC所成的角为60°.

练习册系列答案
相关题目
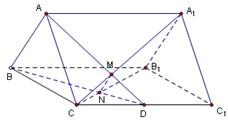 如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,平面ABD和平面A1B1C的交线为MN.
如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,平面ABD和平面A1B1C的交线为MN.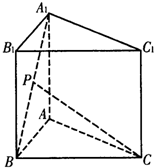 已知正三棱柱ABC-A1B1C的各条棱长都为a,P为A1B上的点,且PC⊥AB
已知正三棱柱ABC-A1B1C的各条棱长都为a,P为A1B上的点,且PC⊥AB 如图,在三棱柱ABC-A1B1C中,已知AC⊥BC,AB⊥BB1,CD⊥平面AA B1B,AC=BC=2.
如图,在三棱柱ABC-A1B1C中,已知AC⊥BC,AB⊥BB1,CD⊥平面AA B1B,AC=BC=2. (2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
(2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=