题目内容
(本小题满分14分)在数列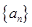 中,
中, 是数列
是数列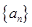 前
前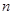 项和,
项和,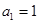 ,当
,当
(I)求证:数列 是等差数列;
是等差数列;
(II)设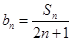 求数列
求数列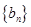 的前
的前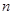 项和
项和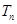 ;
;
(III)是否存在自然数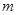 ,使得对任意自然数
,使得对任意自然数 ,都有
,都有 成立?若存在,求出
成立?若存在,求出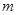 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
【答案】
(I)见解析(II) (III)存在,
(III)存在, 的最大值为
的最大值为 ,理由见解析
,理由见解析
【解析】
试题分析:(I)由已知得,当 时,
时, ,
,
所以 ,又因为
,又因为 ,
,
所以数列 是以1为首项,2为公差的等差数列.
……4分
是以1为首项,2为公差的等差数列.
……4分
(II )由(I)知, ,
,
所以 .
.
所以 ,
……6分
,
……6分
所以

 .
……8分
.
……8分
(III)令 ,显然
,显然 在
在 上是增函数,
上是增函数,
所以当 时,
时, 取得最小值
取得最小值 ,
,
依题意可知,要使得对任意 ,都有
,都有 ,
,
只要 ,即
,即 ,所以
,所以 ,
,
因为 所以
所以 的最大值为
的最大值为 .
……14分
.
……14分
考点:本小题主要考查等差数列的证明,裂项法求和、数列与不等式的综合应用问题,考查学生综合分析问题、解决问题的能力和逻辑思维能力和运算求解能力.
点评:解决此类问题要抓住一个中心——函数,两个密切联系:一是数列和函数之间的密切联系,数列的通项公式是数列问题的核心,函数的解析式是研究函数问题的基础;二是方程、不等式与函数的联系,利用它们之间的对应关系进行灵活处理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)