题目内容
【题目】已知向量 ![]() =(1,2),
=(1,2), ![]() =(﹣3,4).
=(﹣3,4).
(1)求 ![]() +
+ ![]() 与
与 ![]() ﹣
﹣ ![]() 的夹角;
的夹角;
(2)若 ![]() 满足
满足 ![]() ⊥(
⊥( ![]() +
+ ![]() ),(
),( ![]() +
+ ![]() )∥
)∥ ![]() ,求
,求 ![]() 的坐标.
的坐标.
【答案】
(1)解:∵ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() .
.
设 ![]() 与
与 ![]() 的夹角为θ,则
的夹角为θ,则 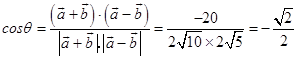 .
.
又∵θ∈[0,π],∴ ![]()
(2)解:设 ![]() ,则
,则 ![]() ,∵
,∵ ![]() ⊥(
⊥( ![]() +
+ ![]() ),(
),( ![]() +
+ ![]() )∥
)∥ ![]() ,∴
,∴ 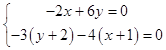 ,
,
解得: 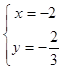 ,即
,即 ![]() .
.
【解析】(1)求得 ![]() +
+ ![]() 与
与 ![]() ﹣
﹣ ![]() 的坐标,利用两个向量的数量积公式、两个向量的数量积的定义,求得cosθ的值,可得
的坐标,利用两个向量的数量积公式、两个向量的数量积的定义,求得cosθ的值,可得 ![]() 与
与 ![]() 的夹角θ的值.(2)根据两个向量垂直、平行的性质,求得
的夹角θ的值.(2)根据两个向量垂直、平行的性质,求得 ![]() 的坐标.
的坐标.
【考点精析】认真审题,首先需要了解数量积表示两个向量的夹角(设![]() 、
、![]() 都是非零向量,
都是非零向量,![]() ,
,![]() ,
,![]() 是
是![]() 与
与![]() 的夹角,则
的夹角,则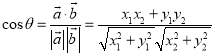 ).
).

练习册系列答案
相关题目