题目内容
设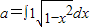 ,对任意x∈R,不等式a(cos2x-m)+πcosx≥0恒成立,则实数m的取值范围为 .
,对任意x∈R,不等式a(cos2x-m)+πcosx≥0恒成立,则实数m的取值范围为 .
【答案】分析:根据定积分几何意义求出a值,根据任意x∈R,不等式a(cos2x-m)+πcosx≥0恒成立,利用常数分离法进行求解;
解答:解:∵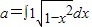 ,表示y=
,表示y=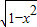 在[0,1]上的积分,也得圆面积的四分之一,
在[0,1]上的积分,也得圆面积的四分之一,
∴a= ×π,
×π,
∴对任意x∈R,不等式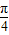 (cos2x-m)+πcosx≥0恒成立,
(cos2x-m)+πcosx≥0恒成立,
可得m≤cos2x+4cosx在x∈R上恒成立,cosx∈[-1,1],
求出cos2x+4cosx的最小值即可,cos2x+4cosx=(cosx+2)2-4,
∵函数开口向上,cosx∈[-1,1],
函数f(cosx)=cos2x+4cosx在[-1,1]上增函数,当cosx=-1时取得最小值,可得(-1)2+4×(-1)=-3,
∴cos2x+4cosx的最小值为-3,
∴m≤-3,
故答案为(-∞,-3];
点评:此题主要考查函数的最值的应用以及定积分的意义,关于函数的恒成立问题,一般用到常数分离法进行求解,是一道基础题;
解答:解:∵
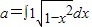 ,表示y=
,表示y=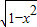 在[0,1]上的积分,也得圆面积的四分之一,
在[0,1]上的积分,也得圆面积的四分之一,∴a=
 ×π,
×π,∴对任意x∈R,不等式
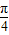 (cos2x-m)+πcosx≥0恒成立,
(cos2x-m)+πcosx≥0恒成立,可得m≤cos2x+4cosx在x∈R上恒成立,cosx∈[-1,1],
求出cos2x+4cosx的最小值即可,cos2x+4cosx=(cosx+2)2-4,
∵函数开口向上,cosx∈[-1,1],
函数f(cosx)=cos2x+4cosx在[-1,1]上增函数,当cosx=-1时取得最小值,可得(-1)2+4×(-1)=-3,
∴cos2x+4cosx的最小值为-3,
∴m≤-3,
故答案为(-∞,-3];
点评:此题主要考查函数的最值的应用以及定积分的意义,关于函数的恒成立问题,一般用到常数分离法进行求解,是一道基础题;

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
设定义域为R的函数f(x)满足下列条件:①对任意x∈R,f(x)+f(-x)=0;②对任意x1,x2∈[1,a],当x2>x1时,有f(x2)>f(x1)>0.则下列不等式不一定成立的是( )
| A、f(a)>f(0) | ||||
B、f(
| ||||
C、f(
| ||||
D、f(
|
设函数f(x)=x|x|+bx+c(b,c∈R),则下列命题中正确的是( )
| A、“b≥0”是“函数y=f(x)在R上单调递增”的必要非充分条件 | ||
| B、“b<0,c<0”是“方程f(x)=0有两个负根”的充分非必要条件 | ||
| C、“c=0”是“函数y=f(x)为奇函数”的充要条件 | ||
D、“c>0”是“不等式f(x)≥( 2
|