题目内容
已知函数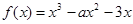 ,
,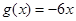 (
(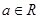 ).
).
(1)若x=3是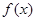 的极值点,求
的极值点,求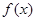 在
在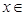 [1,a]上的最小值和最大值;
[1,a]上的最小值和最大值;
(2)若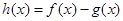 在
在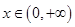 时是增函数,求实数a的取值范围.
时是增函数,求实数a的取值范围.
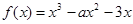 ,
,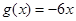 (
(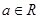 ).
).(1)若x=3是
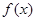 的极值点,求
的极值点,求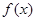 在
在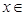 [1,a]上的最小值和最大值;
[1,a]上的最小值和最大值;(2)若
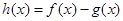 在
在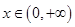 时是增函数,求实数a的取值范围.
时是增函数,求实数a的取值范围.(1) ,
, ;(2)
;(2) .
.
 ,
, ;(2)
;(2) .
.试题分析:(1)由已知可得
 ,从而求得
,从而求得 ;再利用函数的导数求得
;再利用函数的导数求得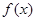 在[1,4]上的最值.
在[1,4]上的最值.(2)由
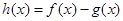 在
在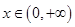 时是增函数,可得
时是增函数,可得 在
在 恒成立;再利用分离参数法将恒成立转化为函数的最值问题加以解决.
恒成立;再利用分离参数法将恒成立转化为函数的最值问题加以解决.试题解析:(1)
 ,由题意得
,由题意得 ,则
,则 ,
,当
 单调递减,当
单调递减,当 单调递增 ,
单调递增 ,
 ;
;  .
. (2)
 ,
,由题意得,
 在
在 恒成立,即
恒成立,即 在
在 恒成立,
恒成立,而

所以,
 .
. 
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
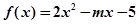 的导函数为
的导函数为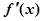 ,若
,若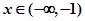 时,
时,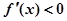 ;
;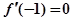 ;
;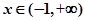 时,
时,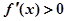 ,则
,则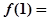 ( )
( )
 ,
, .
. 的极值;(2)若
的极值;(2)若 恒成立,求实数
恒成立,求实数 的值;
的值;
 有两个极值点
有两个极值点 、
、 (
(
 的取值范围,并证明
的取值范围,并证明 .
.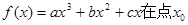 处取得极小值-4,使其导函数
处取得极小值-4,使其导函数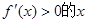 的取值范围为(1,3)。
的取值范围为(1,3)。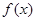 的解析式及
的解析式及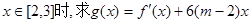 的最大值。
的最大值。 ,函数
,函数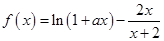 .
.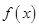 在区间
在区间 上的单调性;
上的单调性;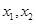 ,且
,且 ,求
,求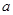 的取值范围.
的取值范围.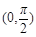 上的函数
上的函数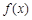 ,
,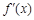 是它的导函数,且恒有
是它的导函数,且恒有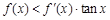 成立,则( )
成立,则( )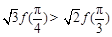
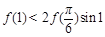
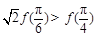
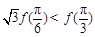
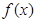 是定义在
是定义在 上的可导函数,其导函数为
上的可导函数,其导函数为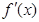 ,且有
,且有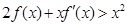 ,则不等式
,则不等式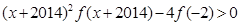 的解集为( )
的解集为( )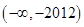
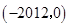

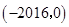
 (a)>
(a)>