Question

如图，四棱锥P﹣ABCD中，PA⊥平面ABCD，PB与底面所成的角为45°，底面ABCD为直角梯形，∠ABC=∠BAD=90°，E是PD的中点，且PA=BC=AD．
（1）求证：CE∥平面PAB
（2）求证：CD⊥平面PAC
（3）若PA=1，求三棱锥C﹣PAD的体积．

Answer 1

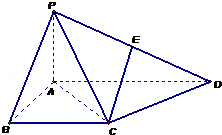
解：（1）取PA的中点F，连接EF，BF，
∵PF=FA，PE=ED，
∴
  ∴ ，
∴四边形EFBC是平行四边形
∴CE∥FB
∵CE?平面PAB，FB?平面PAB
∴CE∥平面PAB
（2）设PA=1，由题意 PA=BC=1，AD=2．                
∵PA⊥面ABCD，
∴PB与面ABCD所成的角为∠PBA=45°．
∴AB=1，
由∠ABC=∠BAD=90°，易得CD=AC= ．
由勾股定理逆定理得 AC⊥CD．                    
又∵PA⊥CD，PA∩AC=A，
∴CD⊥面PAC
（3）由（2）可知，PA⊥面ABCD，
∴三棱锥C﹣PAD的体积就是P﹣ACD的体积，PA=1．
由题意 PA=BC=1，AD=2， PB与面ABCD所成的角为∠PBA=45°．
∴AB=1
S_△ACD= =1，
V_C﹣PAD= = ．