题目内容

如图，已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)，O为原点，点M是椭圆右准线上的动点，以OM为直径的圆与以椭圆长轴为直径的圆交于P、Q两点，直线PQ与椭圆相交于A、B两点，则|AB|的取值范围是
[
2b2
a
，2a)
[
2b2
a
，2a)
．
分析：确定以OM为直径的圆与以椭圆长轴为直径的圆的方程，利用图形的对称性，可知当M在x轴上时，|AB|最小，当M在无穷远时，|AB|最大，由此可求得结论．
解答：解：设M（
a2
c
，m），则以OM为直径的圆的圆心为(
a2
2c
，
m
2
)，半径为|OM|=
(
a2
2c
)2+(
m
2
)2
．
所以圆的方程为(x-
a2
2c
)2+(y-
m
2
)2=
a4
4c2
+
m2
4
①
以椭圆长轴为直径的圆的方程为x2+y2=a2②
根据图形可知，当M在x轴上时，|AB|最小，此时方程①为(x-
a2
2c
)2+y2=
a4
4c2
③
②-③可得：x=c，代入椭圆方程，可得
c2
a2
+
y2
b2
=1，∴y=±
b2
a
，∴|AB|=
2b2
a
．
当M在无穷远时，|AB|最大，以OM为直径的圆与以椭圆长轴为直径的圆交于长轴的端点，∴|AB|→2a
∴|AB|的取值范围是[
2b2
a
，2a)．
故答案为[
2b2
a
，2a)．
点评：本题考查圆的方程，考查圆与椭圆的综合，考查了数形结合的解题思想与极限思想，解题的关键是确定圆的方程，属于中档题．
练习册系列答案
相关题目
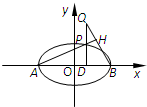如图，已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)过点C(
3
2
，
3
2
)且离心率为
6
3
，A、B是长轴的左右两顶点，P为椭圆上意一点（除A，B外），PD⊥x轴于D，若
PQ
=λ
QD
，λ∈(-1，0)．
（1）试求椭圆的标准方程；
（2）P在C处时，若∠QAB=2∠PAB，试求过Q、A、D三点的圆的方程；
（3）若直线QB与AP交于点H，问是否存在λ，使得线段OH的长为定值，若存在，求出λ的值；若不存在，说明理由．
（2013•汕头一模）如图．已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的长轴为AB，过点B的直线l与x轴垂直，椭圆的离心率e=
3
2
，F1为椭圆的左焦点且
AF1
•
F1B
=1．
（I）求椭圆的标准方程；
（II）设P是椭圆上异于A、B的任意一点，PH⊥x轴，H为垂足，延长HP到点Q使得HP=PQ．连接AQ并延长交直线l于点M，N为MB的中点，判定直线QN与以AB为直径的圆O的位置关系．
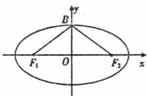（2012•安徽模拟）如图，已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
3
2
，F1，F2分别是椭圆的左、右焦点，B为椭圆的上顶点且△BF1F2的周长为4+2
3
．
（1）求椭圆的方程；
（2）是否存在这样的直线使得直线l与椭圆交于M，N两点，且椭圆右焦点F2恰为△BMN的垂心？若存在，求出直线l的方程；若不存在，请说明由..
（2011•崇明县二模）如图，已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0），M为椭圆上的一个动点，F1、F2分别为椭圆的左、右焦点，A、B分别为椭圆的一个长轴端点与短轴的端点．当MF2⊥F1F2时，原点O到直线MF1的距离为
1
3
|OF1|．
（1）求a，b满足的关系式；
（2）当点M在椭圆上变化时，求证：∠F1MF2的最大值为
π
2
；
（3）设圆x2+y2=r2（0＜r＜b），G是圆上任意一点，过G作圆的切线交椭圆于Q1，Q2两点，当OQ1⊥OQ2时，求r的值．（用b表示）
精英家教网如图，已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)过点(1，
2
2
)，离心率为
2
2
，左、右焦点分别为F1、F2．点P为直线l：x+y=2上且不在x轴上的任意一点，直线PF1和PF2与椭圆的交点分别为A、B和C、D，O为坐标原点．设直线PF1、PF2的斜率分别为k1、k2．
（Ⅰ）证明：
1
k1
-
3
k2
=2；
（Ⅱ）问直线l上是否存在点P，使得直线OA、OB、OC、OD的斜率kOA、kOB、kOC、kOD满足kOA+kOB+kOC+kOD=0？若存在，求出所有满足条件的点P的坐标；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网