题目内容
（本小题满分12分）
已知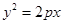
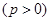，过点
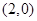作直线与抛物线交于两点，若两点纵坐标之积为
.
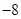(1)求抛物线方程；
(2)斜率为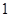
的直线不经过点
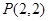且与抛物线交于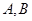
(Ⅰ)求直线
在
轴上截距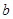
的取值范围；
(Ⅱ)若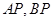
分别与抛物线交于另一点
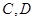，证明：
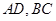交于一定点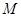
.
【答案】
解：（1）设两交点坐标分别为
，
，因直线经过点
，故有
，即
，化简得
，易知
，
………4分
即抛物线方程为
（2）(Ⅰ)将直线方程
代入得
，由
得
，
又斜率为1经过点
的直线截距为
，
于是直线
在
轴上截距
的取值范围是
………8分
(Ⅱ)设
的坐标分别为
，
则直线
的斜率
，
同理知直线
的斜率分别为
于是由
三点共线得
，
化简得
①
以
替换
得
②
同理由
三点共线得
再由
及
共线分别得到
③
④
将①②式分别代入③④式得
易知
，即
与
交于点
.
………12分
【解析】略
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
